要約:Mathematica グラフィックス入門となる色の使い方について解説する。
名前付きの色
これまでにも紹介し、使用してきたが、Mathematicaでは、次のような色が名前付きの色として定義されており、色の名前で指定できる。名前付きの色には次の25色がある。
Red,Blue,Green,Black,White,Gray,Cyan,Magenta,Yellow,Brown,Orage,Pink,Purpleの13色
Black,Whiteを除く上記から淡い(Light)色:LightRed等(11色)
Transparent:非表示にするための色名
<<プログラム1>>
Graphics[{Red, Disk[{0, 0}, .5], LightBlue, Disk[{1, 0}, .5], Orange,
Disk[{.5, 0.86}, .5], Transparent, Disk[{.5, 0.43}, 1]}]

図1:名前付きの色によるカラー表示
プログラム1による図1では、名前付きの色によるカラー表示を示している。3枚の色付き円盤の上に全体に掛かるようにTransparentの大きな円盤をおいているのであるが、透明なので影響を受けていない。
カラー系列について
Mathematicaでは、次のようなカラーの系列を使うことができる。カラーの系列とは、下表にあるような、光の三原色として有名なRGBcolorなどである。
表:カラー系列
| カラー系列 | 説明 | 使い方 |
| グレー系列 | 白黒の濃淡を表わす。 | GrayLevel[level] level は0から1までの値。 level=0は黒、level=1 は白を表わす。 |
| HUE系列 | 色相、彩度、輝度の3つのパラメータで色を表わす。色相だけでいろいろな色を使うことができ使い方が簡単。 | Hue[h,s,b] h,s,bはそれぞれ、色相、彩度、輝度を示し、0から1までの値。Hue[h]は、Hue[h,1,1]と同じ。 |
| RGB系列 | 光の三原色の強さで色を表わす。感覚的に分かりやすい。 | RGBColor[r,g,b] r,g,bはそれぞれ、赤、緑、青の強度を示し、0から1までの値。 |
| CMYK系列 | 印刷に使うときの表示方法であり、色見本もこれで記述されているので、印刷をする場合は便利である。ただ、パラメータが4つあり、また、色の連続性が感覚と異なる。 | CMYKColor[c,m,y,k] c,m,y,kは、それぞれ、シアン、マゼンダ、黄色、黒の含まれる大きさを示し、0から1までの値。なお、色見本では、通常、%で記述されている。 |
次に上で紹介した色系列の色見本を示す。プログラム2は、今まで使用してきたグレー系列である。グレー系列は、濃淡の1種類の変数(引数)で変化させることができるが、その他については、3から4個の変数があり、一度に変化させて見て頂くことは難しいので、Hue系列については、色相と彩度、色相と明度を変化させた図を、RGB系列については、赤と青、緑と青、緑と赤の混ぜ合わせた図を、CMYK系列については、シアンと黄色を混ぜ合わせた図を一例として掲げた。
なお、プログラム3は、作図の命令がすべて同じであるので、最初の色の定義のみを上げている。
<<プログラム2>>
a=Table[{GrayLevel[i/30],Rectangle[{i,0}, {i+1,1}]},{i,0,30}];
(*グレー系列*)
Show[Graphics[a],AspectRatio->Automatic](*作図*)

図2:グレー系列の色見本
<<プログラム3>>
a=Table[{Hue[i/30,j/30,1],Rectangle[{i,j}, {i+1,j+1}]},{i,0,30},{j,0,30}];
(*彩度を変化させたHue系列*)
Show[Graphics[a],AspectRatio->Automatic](*作図*)
a=Table[{Hue[i/30,1,j/30],Rectangle[{i,j}, {i+1,j+1}]},{i,0,30},{j,0,30}];
(*明度を変化させたHue系列*)
a=Table[{RGBColor[i/30,0,j/30],Rectangle[{i,j},
{i+1,j+1}]},{i,0,30},{j,0,30}];(*RGB系列:赤と青のまぜあわせ*)
a=Table[{RGBColor[0,i/30,j/30],Rectangle[{i,j},
{i+1,j+1}]},{i,0,30},{j,0,30}];(*RGB系列:緑と青のまぜあわせ*)
a=Table[{RGBColor[i/30,j/30,0],Rectangle[{i,j},
{i+1,j+1}]},{i,0,30},{j,0,30}];(*RGB系列:緑と赤のまぜあわせ*)
a=Table[{CMYKColor[i/30,0,j/30,0],Rectangle[{i,j},
{i+1,j+1}]},{i,0,30},{j,0,30}];(*CMYK系列:シアンと黄色の変化の一例*)
(彩度を変化させたHue系列)(明度を変化させたHue系列)
(RGB系列:赤と青のまぜあわせ)(RGB系列:緑と青のまぜあわせ)
(RGB系列:緑と赤のまぜあわせ)(CMYK系列)
図3:カラー系列の色見本の断面
カラー系列の定義
前頁でカラー系列について説明したが、これらを使うことを考えると、グレー系列やHue系列の様に1つの引数で使いたい色が取り出せるようにしておければ、非常に便利である。この様な場合には、カラー系列を定義して使うことができる。
例えば、プログラム5にあるように前頁の彩度を変化させたHue系列で、彩度=0.4のところをpastelという名前で定義すればいい訳である。
<<プログラム4>>
pastel[x_]:=Hue[x,0.4,1];(*カラー系列を定義*)
a=Table[{pastel[i/30],Rectangle[{i,0}, {i+1,1}]},{i,0,30}];
Show[Graphics[a],AspectRatio->Automatic](*作図*)

図4:定義したパステルカラー
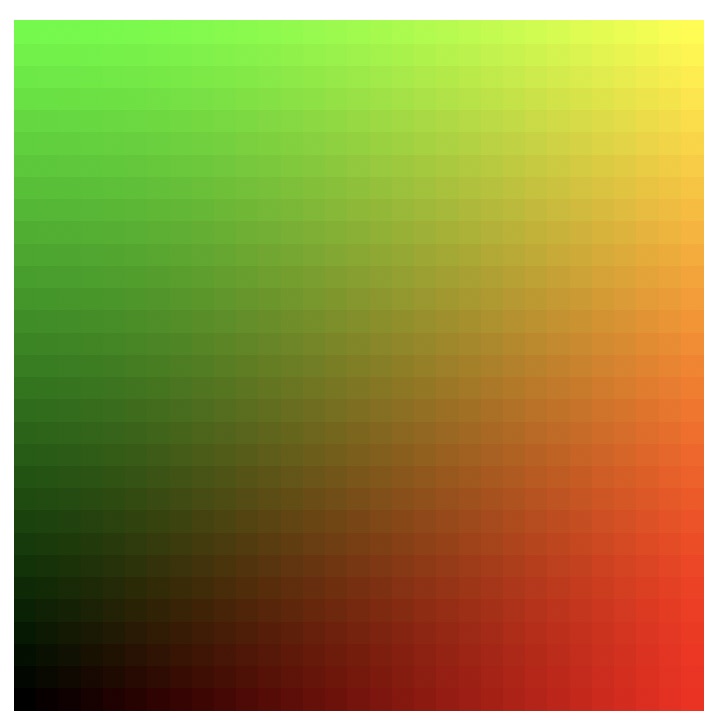
同様に明度を変化させたHue系列で、明度=0.5のところをdeepという名前で定義してみた。Hue系列を使ったパステルやdeepの例は、1つの引数で全ての色相を取り出すことができ、非常に便利である。これとは別に何かのイメージに固有の色を定義する場合には、RGBColorやCMYKColorも使うことができる。プログラム5の例では、春、秋、曙をイメージしたカラー系列を定義してみた。なお、これらを作るときは、カラー口絵に示した正方形のカラーマップをみながら、引数を変化させてカラー系列を定義するのが、便利である。
<<プログラム5>>
deep[x_]:=Hue[x,1,0.5];(*カラー系列を定義*)
a=Table[{deep[i/30],Rectangle[{i,0}, {i+1,1}]},{i,0,30}];
Show[Graphics[a],AspectRatio->Automatic];(*作図*)
springcolor[x_]:=CMYKColor[Mod[x,1],0,Mod[x,1]/2+.5,0];
(*春のカラー系列の定義*)
fallcolor[x_]:=CMYKColor[0,Mod[x,1]/1.3+.1,Mod[x,1]/2+.5,0.05];(*秋色の定義*)
akebonocolor[x_]:=RGBColor[Mod[x,1],0,1-Mod[x,1]];(*曙色の定義*)

図5:定義したカラー系列(上からdeep、春。秋、曙)
上で定義したカラー系列を使用して、図を作成した。図2は、春のカラー系列を使って5角形のを描いてみたものである。グラディエーションが筆者の気に入った。図3は秋のカラー系列を使い、超星(8、3)を重ねて描いたものであるが、ちょうどポインセチアの形となった。図4は四角形と内接円を交互に描いたものを曙カラー系列で色付けした図である。
<<プログラム6>>
rulen[x_List,n_]:=(n*x + RotateRight[x])/(n+1);
springcolor[x_]:=CMYKColor[Mod[x,1],0,Mod[x,1]/2+.5,0];
(*春のカラー系列の定義*)
npolygon[n_Integer]:=
Table[N[{Sin[i/n*2*Pi]/2+.5,Cos[i/n*2*Pi]/2+.5}],{i,1,n}];(*多角形*)
a=npolygon[5];p={};
Do[p=Append[p,{springcolor[i/15],Polygon[a]}];a=rulen[a,20],{i,0,60}];
Show[Graphics[p],AspectRatio->Automatic,PlotRange->{{0,1},{0,1}}];(*図6*)
fallcolor[x_]:=CMYKColor[0,Mod[x,1]/1.3+.1,Mod[x,1]/2+.5,0.05];(*秋色の定義*)
superstar[n_Integer,m_Integer]:=Table[N[{Sin[Mod[m*i,n]/n*2*Pi]/
2+.5,Cos[Mod[m*i,n]/n*2*Pi]/2+.5}],{i,1,n}];(*超星の定義*)
a=superstar[8,3];p={};
Do[p=Append[p,{fallcolor[i/15+.9],Polygon[a]}];a=rulen[a,15],{i,0,30}];
Show[Graphics[p],AspectRatio->Automatic,PlotRange->{{0,1},{0,1}}];(*図7*)
akebonocolor[x_]:=RGBColor[Mod[x,1],0,1-Mod[x,1]];(*曙色の定義*)
a=Table[{akebonocolor[.5-i/10],
Rectangle[{-(1/Sqrt[2])^i, -(1/Sqrt[2])^i}, {(1/Sqrt[2])^i, (1/Sqrt[2])^i}],akebonocolor[i/10],Disk[{0,0},(1/Sqrt[2])^i]},{i,0,10}];
Show[Graphics[a],AspectRatio->1];(*図8*)
図6:春のカラー系列で色付けした五角形の回転 図7:晩秋のポインセチア

図8:曙カラー系列で色付けした四角形と内接円
限定した数色を使う
前頁では、カラー系列を定義して連続して変化する色を使えるようにした訳であるが、数色を限定して使う場合の方が多いかも知れない。そのような時に自分の気に入った数色を限定して使う方法について説明する。
1つ目は、カラー系列の中からMod[]関数等を使って、限定した色しか使えないようにする方法である。
<<プログラム7>>
a=Table[{Hue[Mod[i,5]/5],Rectangle[{i,0}, {i+1,1}]},{i,0,15}];
Show[Graphics[a],AspectRatio->Automatic];(*作図*)

図9:Mod[]関数により限定した数色
上の方法は、使用方法が比較的簡単であるが、色の指定は、数字の間隔に依存して自分が思っているとおりの色が出るとは限らない。この様な場合には、次の方法が利用できる。
2つ目の方法は、限定した色のカラー関数を定義する方法である。プログラム8では、deepcolorという名称でCMYKColorのカラー系列を使って、6種類の色を0から5までの数字に登録している。この方法の利点は、自分の気に入った色を気に入った順番に並べることができる点である。前頁の方法でカラー系列を定義するには、カラーマップの連続したところをカラー系列として定義しなければならなかったが、この方法では、それらの制約がなくなった。ただ、色数が限定されるとともに連続した色の変化とはならない。
<<プログラム8>>
deepcolor[i_]:=Which[i<=0,CMYKColor[1,1,0,.3],
i<=1,CMYKColor[.2,1,0,.3],
i<=2,CMYKColor[0,1,0,.3],
i<=3,CMYKColor[0,1,.3,.3],
i<=4,CMYKColor[0,1,1,.3],
True,CMYKColor[0,.3,1,.3]];(*6種類の色の定義*)
a=Table[{deepcolor[Mod[i,6]],Rectangle[{i,0}, {i+1,1}]},{i,0,11}];
Show[Graphics[a],AspectRatio->Automatic];(*作図*)

図10:選んで定義した色(カラー口絵)
これらの方法を使って、限定した色数で図形を作成した。プログラム8では関数Mod[]を使い2または3種の色を使う方法と限定した色を定義して使う方法を示している。
図11は3種類の白黒の濃淡を図12は10種類の色を定義して使用している。
<<プログラム10>>
rule9[x_List]:=(9*x + RotateRight[x])/10;
n=4;a=Table[N[{Sin[i/n*2*Pi]/2,Cos[i/n*2*Pi]/2}],{i,1,n}];
p=Table[{Hue[Mod[i,2]/2+.3],Polygon[Nest[rule9,a,i]]},{i,0,30}];
Show[Graphics[p],AspectRatio->Automatic,PlotRange->{{-.5,.5},{-.5,.5}}];(*図11*)
n=5;a=Table[N[{Sin[i/n*2*Pi]/2,Cos[i/n*2*Pi]/2}],{i,1,n}];
p=Table[{Hue[Mod[i+j,3]/3+.1],Polygon[Nest[rule9,a,i]]},{i,0,30}];
Show[Graphics[p],AspectRatio->Automatic,PlotRange->{{-.5,.5},{-.5,.5}}];(*図12*)
gray3[i_]:=If[i<=0,GrayLevel[.1],
If[i<=1,GrayLevel[.6],GrayLevel[.8]]];(*濃淡3種類の定義*)
n=3;a=Table[N[{Sin[i/n*2*Pi]/2,Cos[i/n*2*Pi]/2}],{i,1,n}];
p=Table[{gray3[Mod[i,3]],Polygon[Nest[rule9,a,i]]},{i,0,20}];
Show[Graphics[p],AspectRatio->Automatic,
PlotRange->{{-.43,.43},{-.26,.5}}];(*図13*)
deepcolor[i_]:=
If[i<=0,CMYKColor[1,1,0,.3],If[i<=1,CMYKColor[.7,1,0,.3],
If[i<=2,CMYKColor[.5,1,0,.3],If[i<=3,CMYKColor[.2,1,0,.3],
If[i<=4,CMYKColor[0,1,0,.3],If[i<=5,CMYKColor[0,1,.3,.3],
If[i<=6,CMYKColor[0,1,.7,.3],If[i<=7,CMYKColor[0,1,1,.3],
If[i<=8,CMYKColor[0,.7,1,.3],CMYKColor[0,.3,1,.3]]
]]]]]]]];(*10種類の色の定義*)
colorzukei[n_,k_,m_]:=Module[{l,v,p,c},
l=Flatten[Table[
Flatten[Transpose[Table[Range[n]-1,{i,1,j}]]],
{j,1,k-1}]];
v=Transpose[{Cos[l 2Pi/n],Sin[l 2Pi/n]}];
p=Table[Apply[Plus,Take[v,i]],{i,1,n k(k-1)/2}];
c=Table[{deepcolor[Mod[i+4,10]],
npolygon[m,p[[i]]]},{i,1,n k(k-1)/2}];
If[k==1, Show[Graphics[npolygon[m,{0,0}]],
AspectRatio->Automatic],
Show[Graphics[c,AspectRatio->Automatic]];]];(*多角形上への配列*)
npolygon[n_Integer,{x_,y_}]:=Polygon[Table[N[{1.05146*Sin[i/n*2*Pi]/2+x,1.05146*Cos[i/n*2*Pi]/2+y}],{i,1,n}]];
colorzukei[5,5,5](*図14の作図*)
図11:2色に限定した4角形 図12:3色の5角形
図13:白黒の濃淡3種の三角形 図14:5角形による5角形の配列
カラー名で使う
前頁で、色を数字に割り当てて、カラー系列を作る方法について述べたが、色そのものに名前をつけて使用することもできる。名前をつけて登録する方法は、実に簡単である。例えば、RGBColor[1,0,0]をaka(赤)と定義するには、次のようにすればよい。
aka=RGBColor[1,0,0];
また、使い方もRGBColor[1,0,0]の変わりにakaと書けばよい。正方形に色付けをする場合であれば、
Show[Graphics[{aka,Rectangle[{0,0},{1,1}]}]]
カラー名をつけた場合の使い方をプログラム11に示した。この場合は、色に名前を付けたので、色の定義を一括してリストとして取り扱うことができる様になる。
<<プログラム11>>
red=RGBColor[1,0,0];
green=RGBColor[0,1,0];
blue=RGBColor[0,0,1];
yellow=RGBColor[1,1,0];
purple=RGBColor[1,0,1];
colors={red,green,blue,yellow,purple};
rule3[x_List]:=(2.25*x + RotateRight[x])/3.25;
nstar[n_Integer]:=Table[N[{Sin[Mod[2*i,n]/n*2*Pi]/2+.5,
Cos[Mod[2*i,n]/n*2*Pi]/2+.5}],{i,1,n}]
a=nstar[7];
p=Table[{colors[[i]],Polygon[Nest[rule3,a,i]]},{i,1,5}];
Show[Graphics[p],AspectRatio->Automatic]

図15:定義した色名のリストを使う
もう1つの例として、関数の定義の中に入れてしまう方法を示す。この場合は、引き数として色の名前を関数の中に定義しており、描きたい色の名前を入れれば、よい。
<<プログラム12>>
colorzukei[n_,k_,m_,color_]:=Module[{l,v,p,c},
l=Flatten[Table[
Flatten[Transpose[Table[Range[n]-1,{i,1,j}]]],
{j,1,k-1}]];
v=Transpose[{Cos[l 2Pi/n],Sin[l 2Pi/n]}];
p=Table[Apply[Plus,Take[v,i]],{i,1,n k(k-1)/2}];
c=Table[{Switch[color,
red,RGBColor[1,0,0],
green,RGBColor[0,1,0],
blue,RGBColor[0,0,1],
yellow,RGBColor[1,1,0],
purple,RGBColor[1,0,1]],
npolygon[m,p[[i]]]},{i,1,n k(k-1)/2}];
If[k==1, Show[Graphics[npolygon[m,{0,0}]],
AspectRatio->Automatic],
Show[Graphics[c,AspectRatio->Automatic]];]];(*多角形上への配列*)
npolygon[n_Integer,{x_,y_}]:=
Polygon[Table[N[{1.05146*Sin[i/n*2*Pi]/2+x,
1.05146*Cos[i/n*2*Pi]/2+y}],{i,1,n}]];
colorzukei[5,6,6,red](*redを指定*)

図16:色指定の例
透明度による色の変化
Mathematica Ver.6以降、透明度を使用できるようになり、それに伴い色が変化することになったので、それらについても解説する。
プログラムによる図では、RGBcolorの赤、青、黄色の円盤を透明度0.4で重ねたものです。
<<プログラム13>>
Graphics[{Opacity[0.4], Red, Disk[], Blue, Disk[{1, 0}], Yellow, Disk[{.5, 0.86}]}]
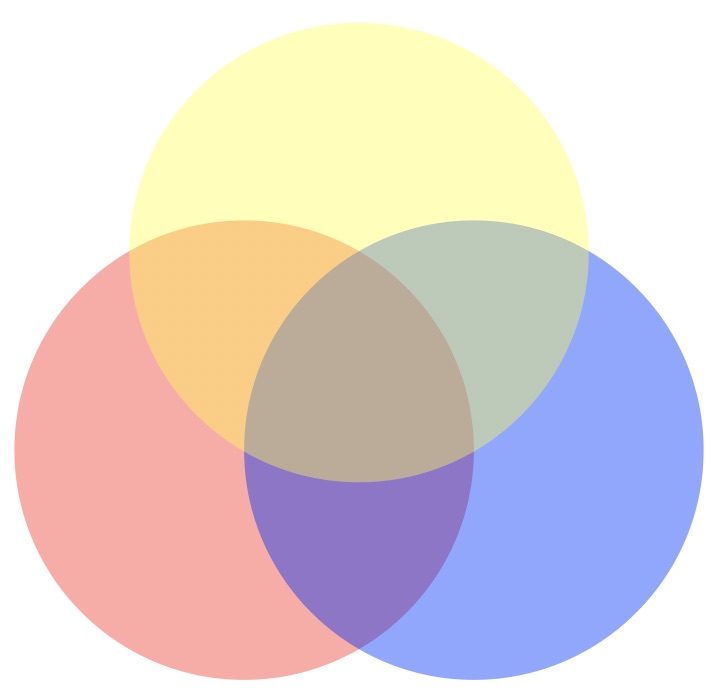
図17:光の3元色を透明度を使い重ねたもの
図17では、光の三原色であるRGBcolorで定義された色であるが、赤、青、黄色が重なった中央部が白になるようなことはありません。つまり、光の三原色を重ねた場合とは違うということです。
最後に面白い例として、色と透明度を変化させた円を150個、重ねたものをプログラムによる図18で示しています。プログラムでは、透明度が含まれた関数Hue[h,u,e,o]を使用しています。ここで、oが透明度を示しています。つまり、Hue[h]=Hue[h,1,1,1] 従って、{Opacity[0.3], Hue[h]}=Hue[h,1,1,0.3]ということです。なお、RGBcolorやCMYKcolorについても透明度が含まれた関数が定義されています。
<<プログラム14>>
a = 0.2;
Graphics[ Table[{Hue[Random[], 1, 1, .3], Disk[{Random[], Random[]}, a Random[]]}, {150}]]

図18:虹色のシャボン玉:透明を使い円盤を乱数で重ねたもの
以上で2次元のグラフィックスに関連する色について解説した。
参考文献:Mathematicaグラフィックスの入門書
中村健蔵「Mathematicaで絵を描こう」1997東京電機大学出版局
ノートブックのダウンロード
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。