要旨:今回は幾何学の根本である対称性について説明します。
富士山の美しさの秘密は対称性
まず、日本人が日本の象徴と考える富士山はなぜ美しいのでしょうか?
いろいろな理由があると思われ、例えば、沼津の海(海抜0m)から日本最高峰(3776m)が一気に臨めます。しかしながら、やはり最大の要因は左右対称の美しい形にあるのではないでしょうか。では、何故、左右対称を美しいと感じるのでしょうか?「それは左右を変えても形が変わらない不変性である。」と言った幾何学者がいらっしゃいました。けだし、名言であると思いますが、さらにチコちゃんはどうして?と質問します。
生物学者に言わせると運動機能的に高い左右対称性を持つ高等生物は、DNAの完全性から生植相手(異性)の左右対称性を美しいと感じるようにプログラムされているのだそうです。
以上が日本の美、幾何学、そして生物学を通しての左右対称性を持つものの美しさについての考察でしたが、今回の視点は異なり、対称性を持たないものをどのようにすれば、対称性を付与できるのかということについて以下説明します。
平面における対称性の基本
まず、平面における対称性(平面群)は17種類が知られていますが、基本となるものは図1に示す3種類で、その他は基本3種類を組みわせたものとなります。

図1:平面における基本的な対称性3種類
対称性を持たないものに対称性を付与するという観点で見れば、図1はFの文字が書かれた1つの図形を平行移動(並進)、鏡に映す(鏡映)、回転させてそれぞれの対称性を付与しようとするわけです。説明する必要はないと思いますが、左右対称は鏡映のことです。回転対称までは、面白いかなと思いますが、並進が対称性に含まれるのは、タイリングする時に必要な操作として含まれているわけで、同じものが並んでいても面白みがない、やぼったいことは言うまでもありません。
さらに幾何学の対称性とデザインする時の対称にはギャップが存在し、それを示す面白い例があります。イスラム文様には8回、10回、12回、14回等の回転対称を持つデザインがあります。幾何学の平面における対称性(平面群)には2回、3回、4回と6回の回転対称性はありますが、それ以外は含まれていません。ここにギャップがあるわけですが、幾何学の対称性で対象となるのは形だけですから、1つの図形のタイリングで14回の回転対称性等は出現しないことを示しており、イスラム文様にある14回の回転対称等がデザインとして存在することとはなんら矛盾しているわけではありません。筆者は幾何学の制約を理解し上手く緩和することで、幾何学デザインがもっと自由になれる一例であると考えています。
さて、幾何学の対称性で対象となるのは形だけであるというお話をしましたが、逆に言えば、形が決まってしまえば、その形が取ることができる対称性は自ずと決まります。図2に正方形の取れる対称性の組合せ(基本を除く)を示しています。

図2:正方形の取れる対称性の組合せ(基本を除く)
では、正方格子において直角二等辺三角形を使って、図3のような図案を作ることを考えてみます。
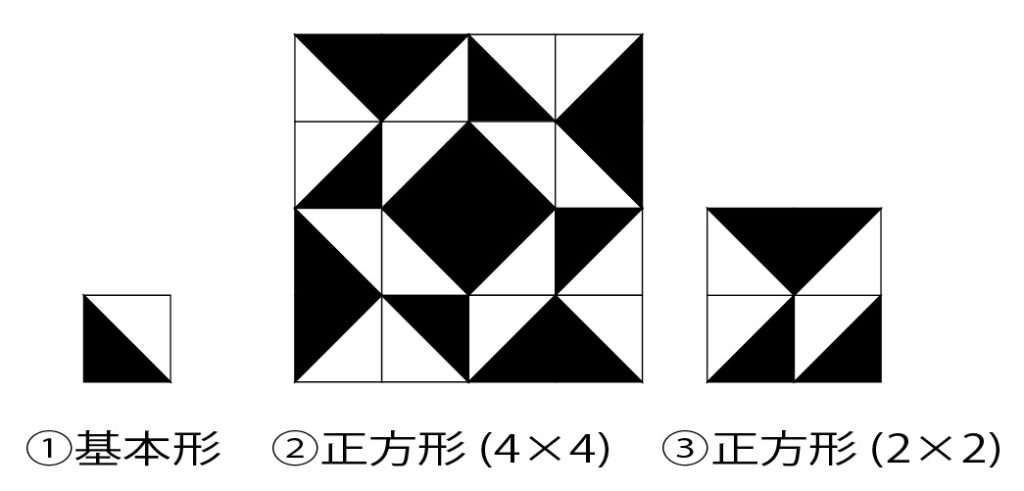
図3:正方格子における図案作成例
図3の左図は基本となる直角二等辺三角形を白黒で塗り分け、組み合せた正方形1つです。中央図が最終的に作りたい正方形4個✖4個の図案例で、面白い図案を作りたいのですが、正方形を回転させると4種類の向きがあるので4を16回掛け合せた数、つまり43億弱の組み合せがあり、全部を描き出すことは到底できません。まずは右図にあるような正方形2個✖2個を作ることにします。
その方法として図4は、図2の正方形の取れる対称性から作り出した図案11個(白黒反転と重複を除く)です。

図4:正方形の取れる対称性から作り出した図案11個
図4で作成した図案だけで十分かどうかを検討するために、図5に正方形2個✖2個の図案128個全種類を示しました。白黒を反転した図案は同じとしたもので、基本図形の左右対称性を考慮すれば、さらに数を減らせますが、いちいち考えているよりも全数作った方が早いと思われます。なお、その分、重複が生じています。

図5:正方形2個✖2個の図案全種類(白黒反転は同じとした)
図4と図5を比較して如何でしょうか?図4も面白い図案になっていますが、流石に図4の11個だけではバラエティが不足することが判ります。
正方形4個✖4個の面白い図案を作る方法
さて、次に筆者秘伝の作り方ですが、正方形4個✖4個の面白い図案を作る時の方法論としては図5の中から気になったものを元に図2の正方形の取れる対称性から作り出すという方法です。この方法で図5の図案1つから作り出した4個✖4個の図案から使えそうな一部を図6に示しました。

図6:図5の図案1つから作り出した正方形4個✖4個の図案の一部
図6左図は基本とした正方形2個✖2個の図案です。いろいろな図案がありますが、如何でしょうか?基本とした正方形2個✖2個の図案1つから出てきた図案とはとても思えないバラエティがあります。さらに群を抜いて面白い図案は右側4個の4回の回転対称の図案でしょう。人間が感じる美とは何なのかを考えた時に、全くの無秩序に美を感じるでしょうか?各自の感じるところですから断定はできませんが、どこかを変えても変えたことさえ気が付かないような無秩序に美を感じることは難しいのではないでしょうか?特に幾何学的なデザインでは、何らかの規則性、ルール、構造を持つものに面白さを感じるのではないでしょうか。そういった意味で4回の回転対称は明確に全体の関連が分かり、さらに動きが感じられます。その他の場合も関連性は感じられますが、4回の回転対称の明確さは圧倒的です。
先ほど、正方形4個✖4個の図案の組み合わせが43億弱であるとお話ししましたが、その中で統一性・関係性・動きが感じられるような図案は殆どなく、大部分は秩序のないものです。その中から面白いものを見つける方法の提案が図6のように図5の図案から図2にある対称性を利用して作り出すことだと考えています。図5の図案128種に図2にある対称性を付与して正方形4個✖4個の図案を作った場合の図案の種類は、図案128種✖対称性の組合せ16✖4方向=8192種類の図案しかありません。43億弱と比べるといかに少なく、いかに効率的に見つけることができるかがお分かりいただけるのではないでしょうか。この他にもいくつかの系統的な作り方がありますが、上で示した方法が最も効率的に作り出す方法と考えています。その他、対称性のない図案で面白い図案は、もちろんありますが、試行錯誤で作り出していく必要があります。
さて、自分でも試してみたいという方は、同じ大きさの小さな正方形4枚を作り、図4左図のように色分けして並べてみると良いでしょう。出来た2✖2図案を元に、紙に書いて4回の回転対称の図案にしてみて下さい。2✖2図案1つが4方向の異なった図案になりますから、思っていたよりもバラエティのある面白い図案になります。なお、コツは次の2つです。
1 正方形を作る時は厚紙を使い、反対側に裏返しても使えるように同じところを黒塗りしておく。
2 2✖2図案を選ぶ時、まとまり過ぎたものを選ばない。反対に自分があまり面白しろくないと思う図案を選んでみて下さい。却ってバラエティが楽しめます。
キルトの図案2つ
図6にある正方形の図案を元にキルトのデザイン案を図7で考えてみました。

図7:図6の図案を元にしたキルトのデザイン案
まず、図6の中から選んだ図案を使い図7左図の縦長長方形の構成を作りました。これを左右対称(鏡映)に配置したものが中央図、2回の回転対称に配置したものが右図です。なお、図案の向きを変えたものもありますが、基本的には同じ図案です。どちらもイメージとしては、「農園は農民夫婦に守られ、四方から押し寄せる外敵等にも負けず、多様な花を咲かせている。」というところでしょうか。
対称性と美を考察
さて、ここでお話は最初に戻ります。つまり、対称性を持つものの美しさについて考えます。図7中央図の左右対称の不変性、言葉を変えれば安定感を善しとするか?右図の2回の回転対称の変化の面白さを好しとするかではないかと考えます。各人の好みとして、それぞれお好きな方を選んでみて下さい。もし、図7中央図と右図の両方に面白さを感じていただけるのであれば、筆者の喜びとするところでしょう。
また、六方格子についても同様な観点がありますが、紙面の制約からここまでとします。
以上で対称性についてのお話は終りです。図案を考える時に対称性との関係をどう捉えたら良いのかについてお話しし、図案を作る時にバラエティの範囲を取りこぼすことなく、試行錯誤の範囲を最小限にできる方法論についてご説明しました。必要以上に難しくしないように対称性の記号等を使わず説明したので、却って解らないところが出たかもしれません。筆者の力不足とご容赦ください。
また、今回の内容について御確認いただきました千葉大学 手嶋教授に感謝いたします。少なくとも嘘はないと確信できて、大いに安心しました。ありがとうございました。
次回は、今回も若干お話ししましたが、イスラム文様風のデザインについて、8回、10回の回転対称という幾何学の対称性を超えたデザインに挑戦してみます。ご期待ください。
参考文献
1 中村健蔵1998年「Mathematicaで絵を描こう」東京電機大学出版局
2 中村健蔵2019『パッチワークキルターのための幾何学デザインシリーズ 幾何学で進化するキルトデザイン』楽天Kobo・キンドルDP


