要約:初心者に向けて、Mathematicaを利用すれば、どんなことが出来るのかを簡単な使用例等で示します。最初は簡単なシミュレーションの例であり、さらに簡単な確率の計算ですが、それらは最終的に図として表示され、理解を助けてくれるでしょう。
1 事故の発生についての簡単なシミュレーション
事故の発生を見ていると、同じような事故が立て続けに2〜3件起こるようなことがよくあります。このような現象を見ていると偶然、このようになったのか、何かの必然で起こったのかが分からなくなります。このような時は次のような簡単なシミュレーションを行ってみると理解を助けてくれるでしょう。
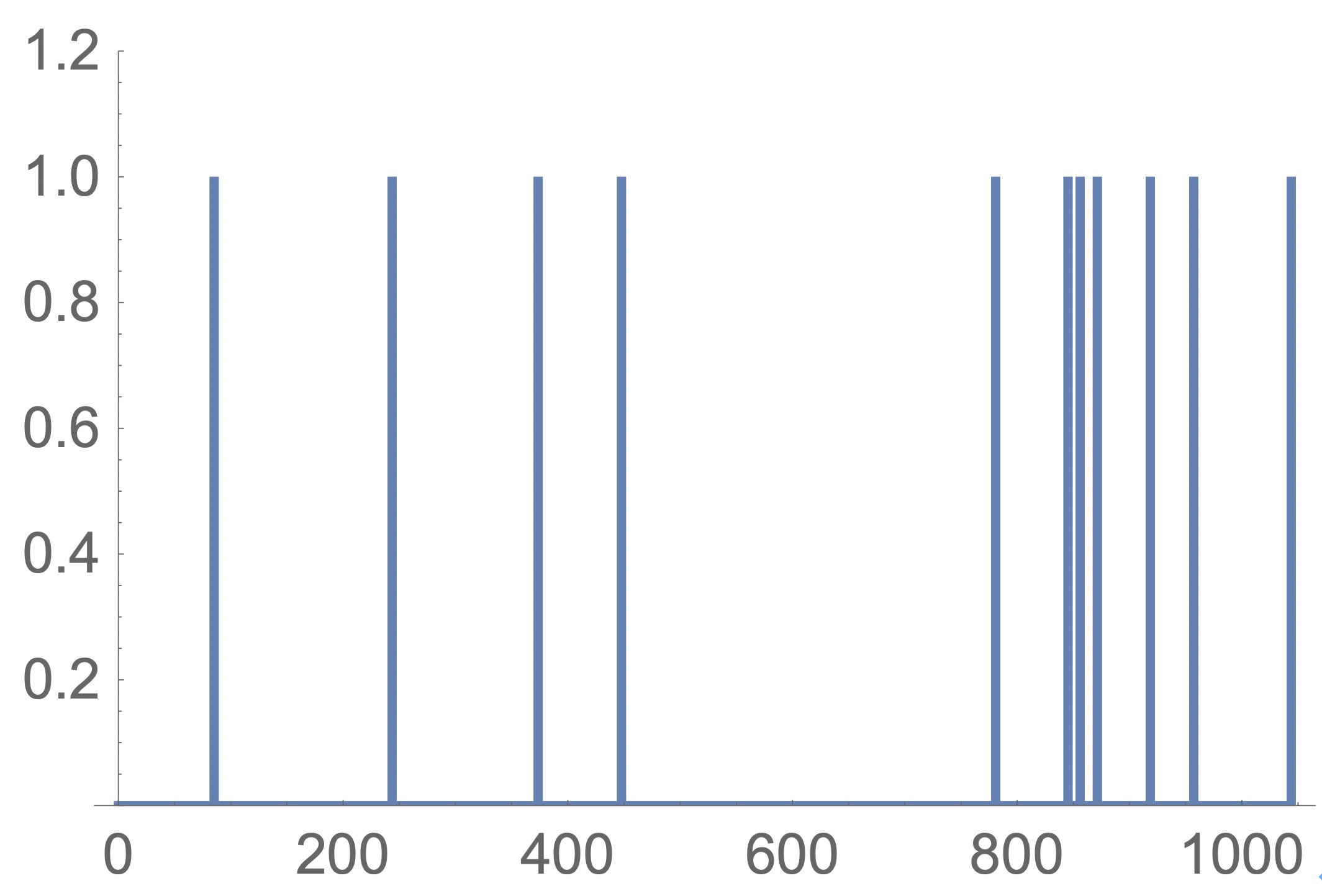
稀な事象の発生時間間隔は、指数分布で近似されることが知られています。図1に平均時間間隔100単位時間の指数分布に従う事象の生起の時間間隔を見ることにします。なお、リスト1は指数乱数を表示するためにリストの操作を行っており、1の値の時に事故が起きたと考えていただきたい。
<リスト1>
exrnd[e_]:=-e*Log[Random[] ];(*指数乱数の関数*)
accident[tmax_,mu_]:=(*リストの操作*)
Module[{alist={{0,0}},t=0},
While[t<tmax,
t=t+exrnd[mu];
AppendTo[alist,{t,0}];
AppendTo[alist,{t,1}];
AppendTo[alist,{t,0}];];
ListPlot[alist,PlotJoined->True,PlotRange->{0,1.2}]];
accident[1000,100](*実行*)
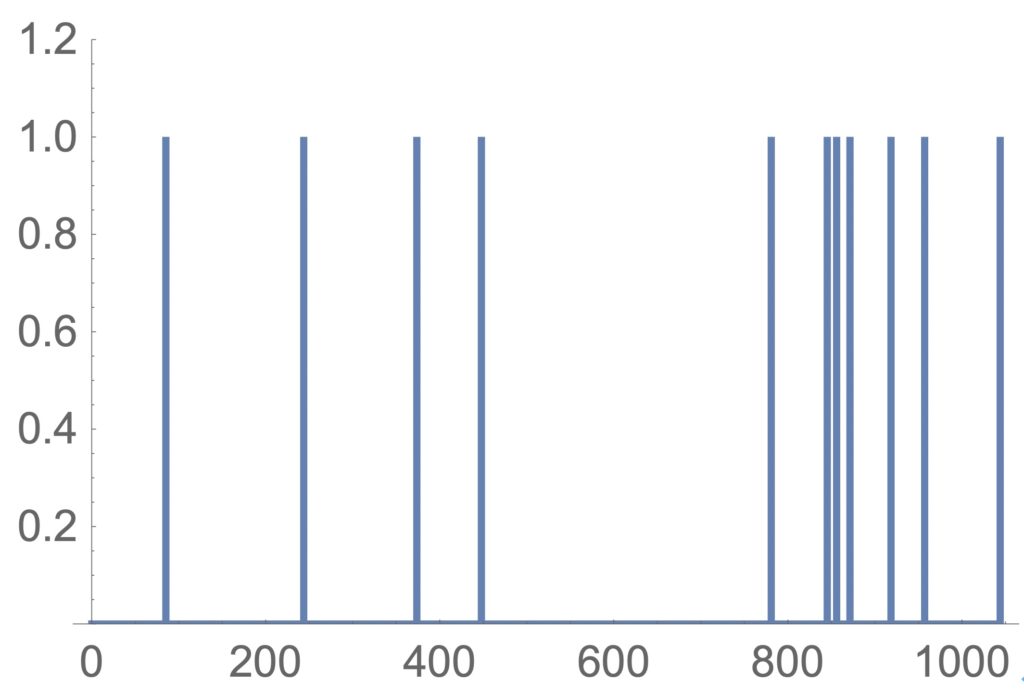
図1:稀な事象の発生の状況
白紙的で、しかも、簡単なシミュレーションですが、図2から平均発生間隔が、100単位時間であっても100単位時間毎に決まって事故が起きるようなことはなく、発生時間間隔は長い場合と短い場合があり、一定間隔で起こったり、900単位時間前後のように立て続けて起こるようにみえます。上のシミュレーションを何度か実際に実行してみると稀な事象は長い目でみれば、上のような調子で起こる傾向があることが理解されるでしょう。
2 あるグループ内で誕生日が一致する確率
学校のクラスなどで誕生日の話が出ると、ある1組が同じ誕生日であることが分かって偶然は良くあるものだと思うような経験をしたことはないでしょうか。
グループの人数に応じる誕生日が一致する人が1組以上いる確率を計算してみましょう。図2に2〜100人の人がいる場合に同じ誕生日の人が1組以上いる確率を示しています。
<リスト2>
bf[n_]:=N[1-365!/365^n/(365-n)!];
ListPlot[Table[bf[i],{i,1,100}],PlotJoined->True]
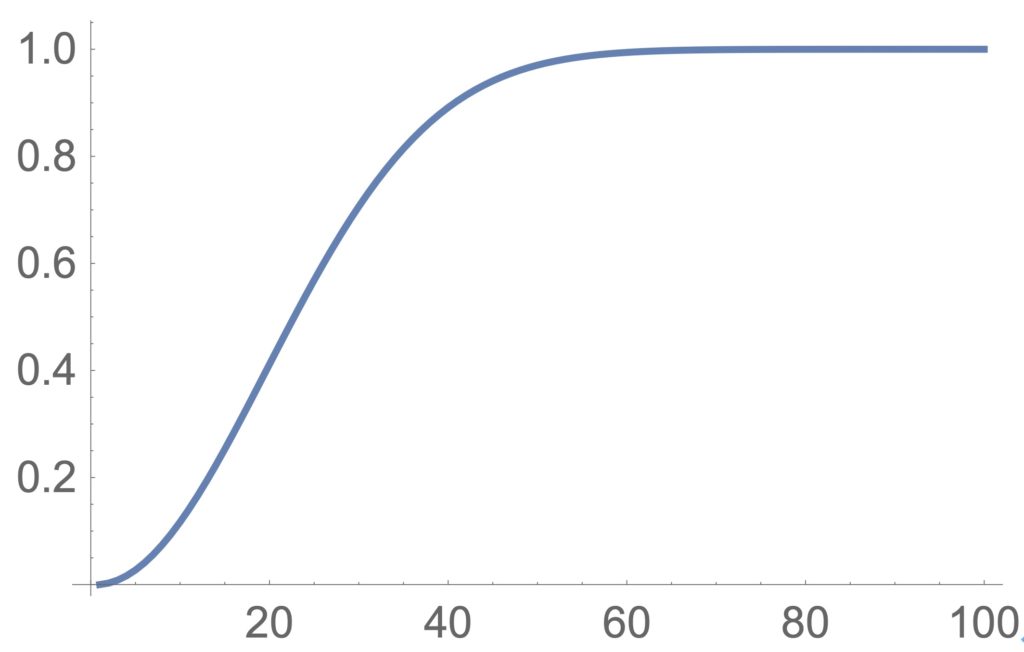
図2:同じ誕生日の人が一組以上いる確率
この結果から読みとれることは、20人では40%程度ですが、34人もいれば80%以上であり、45人以上ではほぼ確実にいると考えられます。したがって、昔の40人クラスであれば、いないほうが珍しいわけです。
では、これがどうして起こるのかを関係の数から見ていきましょう。関係の数とは、2人の人がいれば、1対1の関係が1つあるということです。1人増えて3人になると関係の数は2増えます。同様にn人がn+1人になると関係の数はn増えます。これを式にして再帰的な計算をしても良いわけですが、n人の関係の数は1からn-1の整数を足したものと考えれば、第1項で計算したことが大いに活かせることになるわけです。
r[k_] := k (k – 1)/2
r[2]
1
Plot[r[i], {i, 2, 100}]

図3:人数に応じる関係の数
ある2人の誕生日が同じである、つまり、1つの関係において誕生日が同じである確率は365分の1です。従って、関係が365ある時に誕生日が同じである関係が1つあることが期待されるという表現で説明されます。では、その辺りの関係の数と確率を数値で算定すると次のようになります。
Table[{i, bf[i], r[i]}, {i, 20, 45, 5}]
{{20, 0.411438, 190}, {25, 0.5687, 300}, {30, 0.706316, 435},
{35, 0.814383, 595}, {40, 0.891232, 780}, {45, 0.940976, 990}}
先ず、20人の時、関係の数は190、その後、5人ずつ増えるに従い、関係の数は1.5倍と急激に増えていき、それに従い、確率も急激に増えていきますが、40人を超えるとだんだんと飽和していきます。これから同じ誕生日の人が一組以上いる確率が20人あたりから急激に増えるのは、関係の数が急激に増えるためであることがわかりました。そして、その後も急激に増えるために、急激に1に飽和していくわけです。
3 マージャンの配牌
マージャンの配牌は何通りくらいあるでしょうか。つまり、麻雀で最初に配られた時の組み合わせの総数を計算してみましょう。この計算は、第2章の順列組み合わせで再度説明しますが、重複組み合わせと呼ばれるもので、案外簡単なものであり、その解法に従うと、次のように解くことができます。麻雀の牌はすべて4個1組で34種類の牌から13個を取り出したときの組み合わせは(1+X+X2+X3+X4)34の展開式におけるx13の係数に等しいことが分かっています。この式を使い、配牌の組み合わせの総数を計算してみます。
<リスト3>
Coefficient[Expand[(1+x+x^2+x^3+x^4)^34],x,13];
98521596000
すなわち、麻雀の配牌は約985億通りの組み合わせがあります。
麻雀の配牌の計算はいろいろ本で調べても、なかなか見つけることができなかったので、自分でやってみると簡単なので驚いた記憶があります。よく考えてみると、この計算はMathematicaを使えば簡単ですが、FORTRAN等の従来型の計算機言語による計算は、ほとんど困難であることが予想されます。このように従来の数学の本では理論のみを教えるものですが、この本では理論だけではなくメソッド(方法)も併せて記述することができるのではないかと思い、俗な話題ですが例としてあげた次第です。
まとめ:Mathematicaを使えば簡単に計算でき、しかも、簡単に図にできることの例として示しました。
参考文献:Mathematicaの入門書
1 Stephen Wolfram “An Elementary Introduction to the Wolfram Language” 2017 Wolfram Media
2 C・ヘイスティング「ハンズ・オン・スタートMathematica」2019丸善
3 中村健蔵2019『MathematicaによるOR』楽天Kobo・キンドルDP