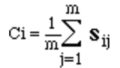要約:最も簡単な2次元のグラフィックス・プリミティブである点Pointを使って簡単な図を描くことを解説します。
はじめに
Mathematicaは、数式処理システムと呼ばれるもので、数値計算だけでなく数式での解答も出してくれるものです。しかも、グラっフィクスの機能も高く、二次元・三次元の図・アニメーションを作ることができます。
ここでは、最も簡単な2次元のグラフィックス・プリミティブとして点Pointを使って簡単な図を描くことを解説しています。
なお、Mathematicaが初めてという方は、概論として何ができるかを説明していますので、そちらを見て下さい。
また、全く使ったことがない方には、最初に使う時に重要な点と学びはじめに知っておくと後で苦労しない重要な概念を説明していますので、そちらをご覧ください。
点のグラフィックス・プリミティブについて
グラフィックス・プリミティブは、グラフィックの元になる基本要素といった意味です。最後にもう少し詳しく説明します。まずは最も簡単な2次元のグラフィックス・プリミティブとして点Pointについて説明します。
Point[{x,y}] が点を表す関数で、位置{x,y}にある点を示しています。
Graphics[Point[{0, 0}]] の形で原点にある点を表示できます。※図省略
前回説明したリストを作る関数Tableを使って、等間隔で10✖️10個並べたものが下です。
Graphics[Table[Point[{i, j}], {i,1, 10}, {j, 1,10}]] ※図省略
大きさと色をつけた点の配列
ここまでは、図は省略しました。
Pointには位置以外にも属性があり、大きさと色をつけることが出来ます。
fig1 = Graphics[ Table[{PointSize[(i + j)/130], Red, Point[{i, j}]}, {i, 1, 10}, {j, 1, 10}]]

図1:縦横均一な点の配列(赤)
もう1つ別の図を作成した後に説明します。
fig2 = Graphics[ Table[{PointSize[(Abs[i – 5] + Abs[j – 5])/130],
Blue, Point[{i, j}]}, {i, 1, 10}, {j, 1, 10}]]

図2:縦横均一な点の配列(青)
点の大きさはPointSize[a]で指定します。Aは0を含む正数で、全体との比率で表されます。目安としては、0.02が細かい点となります。fig1では、左下から上・右にいくに従い徐々に大きくなり、右上で最大となるようにi+jを適当な数で割っています。fig2では中央から外側に行くと大きくなるように絶対値の関数Absを使い、Abs[i – 5] + Abs[j – 5]を適当な数で割っています。色については、後ほど別の回で説明しますが、ここではとりあえず、赤(Red)と青(Blue)を使っており、Pointの前において色を指定していると考えて下さい。
なお、ここでの注目点はTableの使い方で多重構造のリストを作っていることです。下の例は、最も簡単な2✖︎2の多重構造を作る例です。
Table[{a, b}, {j, 2}]
{{a, b}, {a, b}}
折角、図をfig1, fig2で指定したので、重ね合わせて表示します。そのために使用するのが、Showです。もちろん、表示範囲を合わせることが必要で、適当に書いたグラフ2つを同時に表示しようとしても上手くいかないことは当然です。
Show[fig1, fig2]

図3:図1に図2を重ねた図
もちろん順番(重ね方)を変えると見た目が変わるので、やってみて下さい。
等間隔でない配列
ところで、今までの図は全て点の位置が等間隔に配置されたものでしたが、点の位置を変化させることを考えて見ましょう。図4は間隔を2乗、3乗の比率で、図5は整数への繰り上げを利用して位置を変化させたものです。

図4:間隔の変更(2、3乗) 図5:間隔の変更(繰り上げ)
Show[Graphics[Table[{PointSize[0.001*i*k],
Point[{k^2/10,i^3/100}]},{i,1,10},{k,1,10}]],AspectRatio->1];(*図4*)
Show[Graphics[{PointSize[0.03],Table[Point[{i+Mod[k+1,2]/2.0,
k+Mod[i+1,2]/2.0}],{i,1,10,0.5},{k,1,10,0.5}]}],AspectRatio->1];(*図5*)
図4では、Point[]の位置の指定にも、変数の積を直接使っています。そして、その値を1から10までの範囲に納まるように2乗は10分の1に、3乗は100分の1にしています。
図5では、関数Mod[]を使い点の位置にリズムを付けています。この関数は、Mod[i,n]の形式でiをnで割った余りを答えとして返してくれます。例えば、Mod[i,3]でiを1から10まで変えると下表のように値を返します。Mod[i,2]も下表のとおりです。
表:関数Mod[]の使い方
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Mod[i,3] | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
| Mod[i,2] | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
従って、i+Mod[k+1,2]/2.0で点の位置を与えると図のようにリズミカルな変動を与えることができます。
ListPlot[Table[N[{i,i+Mod[i+1,2]/2.0}],{i,1,10,0.5}],PlotJoined->True]
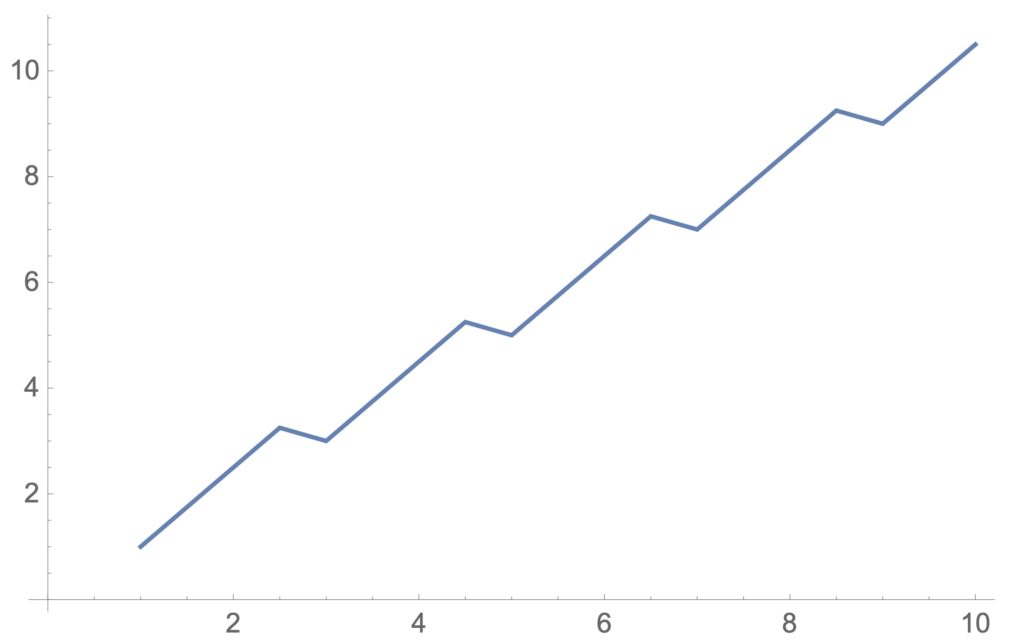
図6:関数Mod[]によるリズミカルな変動
点の大きさの指定方法について
ところで、点の大きさの指定法として今まで紹介してきたPointSize[]の他に、AbsolutePointSize[]を使い指定することができます。PointSize[]が図の大きさの比率で点の大きさを指定することと比較して、AbsolutePointSize[]はポイント数(1ポイントは1/72インチ)で点の大きさを指定できます。ここで図7を見て下さい。MathematicaのP C画面上では、描いた図の大きさを自由に変化することができるのですが、図7では点の大きさを2つの指定法で指定し、図の大きさを変更した場合の見え方の違いを比べています。

図7:点の大きさの指定法による違い(右図は大きさを半分にしたもの)
Show[Graphics[
{Table[{PointSize[0.001*i*k],Point[{k,10-i}]},{i,1,10},{k,1,5}],
Table[{Red,AbsolutePointSize[0.32*i*k],Point[{k,10-i}]}, {i,1,10},{k,6,10}]}],AspectRatio->1];
図7の右半分の赤部分が、AbsolutePointSize[]を用いて点の大きさを指定したものです。大きい図では左右が同じようにだんだん大きくなって見える点の大きさが、図の大きさを半分にすると赤部分の点の大きさは変化しないため、全体の見た目は変わってしまうことになります。PointSize[]とAbsolutePointSize[]のどちらが使いやすいかは、主観の問題になるかもしれないが、Mathematicaに絵を描かせて絵の全体の大きさも見た目で変化させ、全体の中でのバランスを考えて点の大きさを指定する場合には、PointSize[]が使いやすいでしょう。従って、今まではAbsolutePointSize[]を使わず、PointSize[]を使っていました。一方、図の大きさが一定で変えることのない場合には、AbsolutePointSize[]が便利かもしれません。
まとめ
以上が点の関数Pointの簡単な使い方です。まとめると次の通りです。
・点の関数Point[{x,y}]。位置{x,y}の点を示す。
・PointSize[a]で点の大きさを指定できる。aは0を含む正数、0.02で細かい点。
・色は関数Pointの前に置いて指定できる。
・Graphics[{PointSize[0.05], Red, Point[{1, 1}]}]で位置{1,1}にある大きさ0.05、赤色の点を表示させることができる。
・その他、色々な関数を使って、等間隔でない配列も作ることができます。
最後にグラフィックス・プリミティブについて説明します。グラフィックス・プリミティブは、説明したPoint関数のようなグラフィックを構成する要素の1つです。これらは全て3次元のグラフィックス・プリミティブとして定義されています。つまり、点はPoint[{x,y,z}]で示されますが、2次元でも使えるように定義されています。ただし、2次元では使えないものもあります。例えば、立方体を示すものは2次元としては使えないわけです。この解説では、2次元のグラフィックを対象としているので、以降、2次元としては使えないものを除いたグラフィックス・プリミティブ、いわば、狭義の2次元のグラフィックス・プリミティブを紹介していきます。具体的には、直線Line、円Circle、円板Disk、多角形Polygon、文字列Text等について次回から順番に説明していきます。
参考文献:Mathematicaグラフィックスの入門書
中村健蔵「Mathematicaで絵を描こう」1997東京電機大学出版局
ノートブックのダウンロード
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。