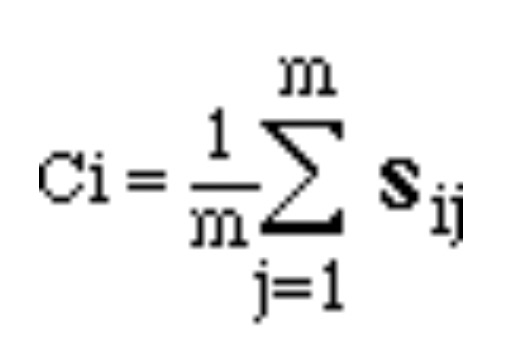要旨:「MBA取得のためのMathematica」の開始に当たり、内容の概要について述べ、最初の意思決定論について説明する。
なお、ノートブックのダウンロードについては末尾から出来ます。
概論
M B Aは経営学修士と言われる学位ですが、組織・企業の進むべき地位・役割・目的を確立し、その目標の合理的実現に向かって各職務・部門の活動を最高度に発揮させる「総合的管理能力」を育成するための教育・訓練と言われています。また、幅広い知識を得るだけでなく、授業の多くはケースメソッドで行われます。筑波大学大学院ビジネス科学研究科(2020年3月現在)の基礎科目と専門科目が、履修内容を知るために科目名が分かりやすいので、下表を見て下さい。
基礎科目
| 経営基礎 | ビジネス数理 |
| ファイナンス基礎 | 計算機科学基礎 |
| 会計基礎 | ビジネスと情報 |
専門科目
| トップレクチャーI&II | オブジェクト指向プログラミング | 財務会計 |
| 計算機科学 | 情報セキュリティ | 技術経営論 |
| ビジネスゲーム | 人工知能とビジネス情報分析 | 最適化モデル |
| 消費者行動 | データマイニング | データ解析 |
| 現代マーケティング論 | インターネットとビジネス情報分析 | 多変量解析 |
| マーケティングリサーチ | アルゴリズム | 統計モデル |
| マーケティングサイエンス | テキストマイニング | プロジェクト・マネジメント |
| 経営戦略論 | ソフトウェア工学 | 会計情報分析 |
| 経営組織論 | 社会シミュレーション | オペレーションズ・リサーチ |
| 組織文化とリーダーシップ | 要求工学 | プログラミング |
| 人的資源管理 | 社会調査法 | ユーザインタフェース |
| インベストメントサイエンス | 非営利組織マネジメント | 情報システムとWeb技術 |
| ファイナンス工学 | 人材育成論 | 企業ガバナンスとマネジメント |
| 金融リスク分析 |
これらの科目から経営工学等による数理的な管理を基礎として、その上に経営論、組織論、人材育成管理、技術管理といったものが組み立てられていることが分かります。また、ケースメソッドを重視しており、後期では演習等が行われます。
このページでは、MBA:経営学修士を学ぶために必要な意思決定論、ゲーム理論、確率・統計、線形計画法、データサイエンス、シミュレーションといった数学的な内容について記述していきます。今後、MBA取得を考えている方は内容を理解するとともに、Mathematicaの使えるPCを持って授業に臨むことで、配布しているノートブックを活用し、宿題だけでなくケースメソッドや演習等の際にツールとして大きな力になるものと考えています。
意志決定論
1 全 般
M B Aでは組織・企業の現在から将来への戦略を決めていかなければなりませんが、その意思決定というものについて考察しておく必要があります。人の考えは十人十色ですが、ある程度合理的に考えた時に考えられる決定の尺度を考察したものが、意思決定基準と呼ばれるものです。
次にA H Pについては、個人の感覚=直感を数値化しようという試みで、多くのものがある場合でも2つのものだけの比較をして、それを統合することで全体的にも整合性のある重み付けをすることができるというものです。
最後のDEMATELはある問題に関連する要因間の関係性を明らかにすることで、人間の考え方を図示しようとするものです。
なお、現在、人工知能は飛躍的に発展し、金融工学や軍事分野では高速な自動決定システムが構築されていますが、経営工学とのハイブリッドとして作られるものが多数を占めています。その観点から意思決定システムを構築・使用する際に意思決定基準・意思決定論は知っておかなければならないものになるでしょう。
2 意志決定基準
不確実さを考慮した意志決定を考える場合には自分の立場における意志決定基準(視点)を明確にすることが重要です。従来知られている意志決定基準には、ラプラスの基準・マクシミン基準・フルビッツ基準・ミニマックス基準(意志決定基準とはとても言えませんが、賭博師的基準)などがあります。これらについて休日の過ごし方を選ぶことを例として説明します。
我家では下のような案を考えましたが、週末の天気によって満足度が左右されるので、レジャー案毎の満足度は下表のように考えました。
表1 レジャー案と満足度
| 天候案 | 晴れ | 曇り | 雨 |
| 映画観賞 | 60 | 60 | 50 |
| ディズニーランド | 80 | 80 | 30 |
| ヨット遊び | 80 | 90 | 0 |
satisfy={{60,60,50},{80,80,30},{80,90,0}};
MatrixForm[satisfy](*行列の形式で出力*)
60 60 50
80 80 30
80 90 0
2.1 ラプラスの基準
各案毎の満足度sijの平均が最大のものを採用する基準です。ある案iの基準は次の式で示されます。ここでjは天気の状態です。
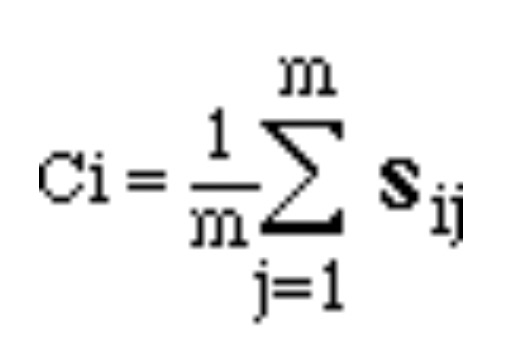
上の例で考えると、
Print[“No. ラプラスの基準値“];
Do[Print[i,” “,Apply[Plus,satisfy[[i]] ]/3.],{i,3} ]
No. ラプラスの基準値
1 56.6667
2 63.3333
3 56.6667
ディズニーランドに行く案が基準値最大となり採用されることになります。
このラプラスの基準は、天候の生起確率を分からないものとして等確率で期待値を取ったものと考えることができます。
2.2 マクシミン基準(悲観論的基準)
最悪の条件を考えて、その中で最も満足度の大きいものを選ぶ基準です。つまり、基準値としては各案の中の満足度最小のものが選ばれる。従って、悲観論的基準といえるでしょう。
Print[“No. マクシミン基準値“]
Do[Print[i,” “,Min[satisfy[[i]] ] ],{i,3} ]
No. マクシミン基準値
1 50
2 30
3 0
上の例では、映画に行くことが最も安全策となります。
2.3 マックスマックス基準(賭博師的基準)
上のマクシミン基準の正反対が、マックスマックス基準であり満足度最大のものを選ぶものです。つまり、基準値としては各案の中の満足度最大のものが選ばれる。従って、賭博師的基準といえるでしょう。
Print[“No. マックスマックス基準値“]
Do[Print[i,” “,Max[satisfy[[i]] ] ],{i,3} ]
No. マックスマックス基準値
1 60
2 80
3 90
上の例では、ヨットに行くことが大穴として採用されることになります。
2.4 フルビッツ基準
マックスマックス基準(賭博師的基準)とマクシミン基準(悲観論的基準)を統合したものが、フルビッツ基準です。即ち、基準値は次の式で示されます。
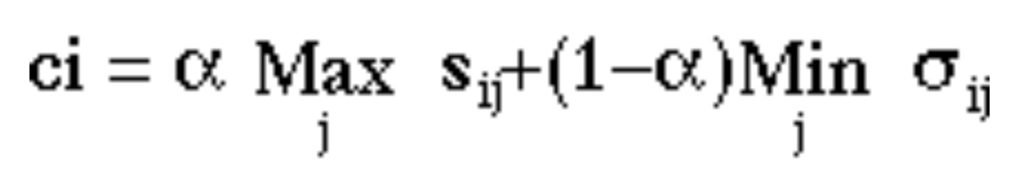
この基準は上の式から分かるように悲観と賭け師の基準を混合したもので、αが混合の程度のパラメータです。
a=.5;(*混合度のパラメータ*)
Print[“No. フルビッツ基準値“];
Do[Print[i,” “,a*Max[satisfy[[i]] ]+(1-a)*Min[satisfy[[i]] ]],{i,3} ]
No. フルビッツ基準値
1 55.
2 55.
3 45.
αの値を50%にした場合、映画とディズニーランドに行くことが同じ点になりました。
2.5 ミニマックス基準(残念さ最小基準)
表2は、各行の最大からの差を取ったものです。これは残念さの大きさを表していると考えられます。つまり、晴れたのに映画観賞をしてしまった場合、ディズニーランドやヨット遊びができなくて残念に思うわけですが、その残念さの大きさを示していると考えられます。
表2 残念さの表
| 天候案 | 晴れ | 曇り | 雨 |
| 映画観賞 | 20 | 30 | 0 |
| ディズニーランド | 0 | 10 | 20 |
| ヨット遊び | 0 | 0 | 50 |
regret=Transpose[satisfy];(*行と列の入れ替え*)
regret=Transpose[Table[
Max[regret[[j]] ]-regret[[j]][[i]] ,{j,3},{i,3}] ];(*残念さの算出*)
MatrixForm[regret](*行列の形式で出力*)
20 30 0
0 10 20
0 0 50
この残念さを最小にする基準が残念さ最小の基準です。つまり、各案の残念さの最大値を基準値として、その中から最小のものが選ばれる。上の例では、
Print[“No. 残念さ最小基準値“];
Do[Print[i,” “,Max[regret[[i]] ] ],{i,3} ]
No. 残念さ最小基準値
1 30
2 20
3 50
この中で最小の残念さです。ディズニーランドに行くことが選ばれるわけです。
天気による満足度という仮定の範囲内だけで考えても、フルビッツ基準まで勘案するとまさに十人十色以上の色々な判断基準・価値基準があることが分かって頂けたことと思います。今後、重要な意思決定をしていくための何かの参考になれば、幸いです。
3 AHP(Analytic Hierarchy Process)
AHP(Analytic Hierarchy Process,階層構造に基づく分析法)は、意志決定において数量化の難しい個人の感覚=直感を数量化しようとする試みです。本節では、AHPの計算をMathematicaで行なう方法を述べます。まず、具体例として面積比をAHPで算定する例をみてみましょう。
3.1 4ヵ国の面積比
図1はMathematicaを用いてリスト1により描いたフランス・ドイツ・オーストリア・スイス、4ヶ国の地図です。
<<リスト1>>

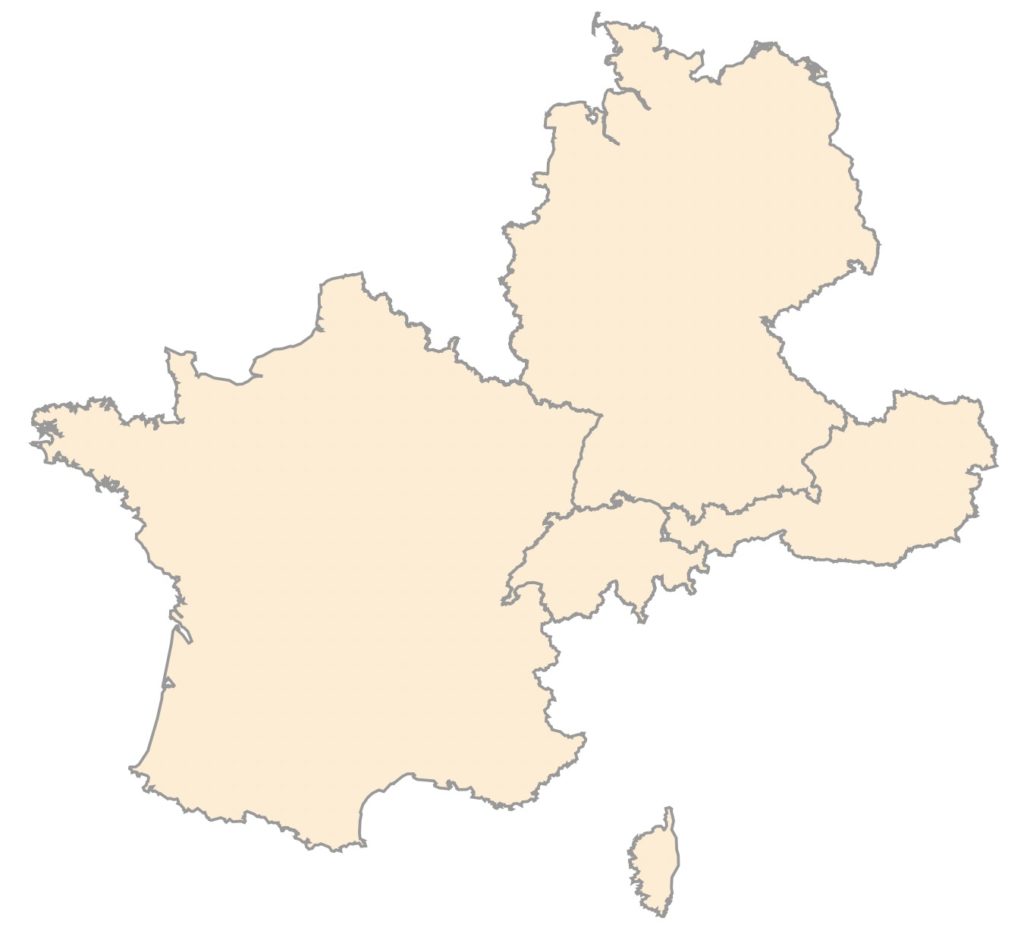
図1:4ヶ国の地図
図1の4ヶ国の面積の比を直感で考えてみていただきたい。例えば、一番小さなスイスを1とすると、オーストリアが2、ドイツが7、フランスが10くらいでしょうか。従って、フランス・ドイツ・オーストリア・スイスの面積比は、5:3.5:1:0.5となります。
これは、全くの当てずっぽうですが、もう少し科学的に、しかも正確にできる方法としてAHPが1971年、ピッツバーグ大学教授T.L.Saatyにより考案されました。この方法は、人間は2つの物の比較(一対比較)なら比較的正確にできることから、要素毎の一対比較から全体の比較を正確に算定しようというものです。AとBを比較した場合Bが大きい場合に記入すべき度数を表3に示しています。なお、Aが大きい場合には、逆数を代入します。
表3:AHPにおいて比較と記入する数字
| 同じ | やや大きい | 大きい | 非常に大きい | 極めて大きい |
| 1 | 3 | 5 | 7 | 9 |
上の例で考えれば、フランスはスイスより極めて大きいので、9。ドイツはフランスよりやや小さいので、1/3。このように1つ1つを比較して表4の行列を完成させます。
表4:一対比較の結果(4ヶ国の面積比)
| フランス | ドイツ | オーストリア | スイス | |
| フランス | 1 | 3 | 7 | 9 |
| ドイツ | 1/3 | 1 | 6 | 8 |
| オーストリア | 1/7 | 1/6 | 1 | 3 |
| スイス | 1/9 | 1/8 | 1/3 | 1 |
この行列からAHPを用いてリスト2により、4ヶ国の面積比を出すと、0.573:0.307:0.079:0.040となります。なお、このリスト2は、分かり易いようにMathematicaのコマンドを並べて書いたものです。
<<リスト2>>
(*1 入力データ*)
n = 4;
ahpdata = {{1,3,7,9},{1/3,1,6,8},{1/7,1/6,1,3},{1/9,1/8,1/3,1}};
(*2 要素の重み付け*)
lmax=First[Eigenvalues[N[ahpdata]]](*最大固有値*)
4.20534
weightvecter=First[Eigenvectors[N[ahpdata]]];(*最大固有ベクトル*)
weight=weightvecter/Apply[Plus,weightvecter](*要素の重み*)
{0.573183, 0.307663, 0.0790646, 0.0400893}
(*3 矛盾のチェック*)
ci = ( lmax – n)/(n-1)(*整合度*)
0.0684452
rcoef={0,0,.58,.9,1.12,1.24,
1.32,1.41,1.45,1.19,1.51,1.53};(*係数*)
cr = ci/rcoef[[n]](*整合比*)
0.0760503
実際の面積比は、0.53:0.34:0.081:0.039ですので、なかなか良い直感です。
なお、矛盾しているかどうかは、リスト2に示した整合度と整合比が、0.1以下(要素数が多くなった場合の最大でも0.15以下)かどうかでチェックできます。
3.2 AHPの数学的背景
要素の数をn、各要素の重みをwi、重みのベクトルをW、一対比較した結果の行列をAとすると、それらは、次の式で表わされます。
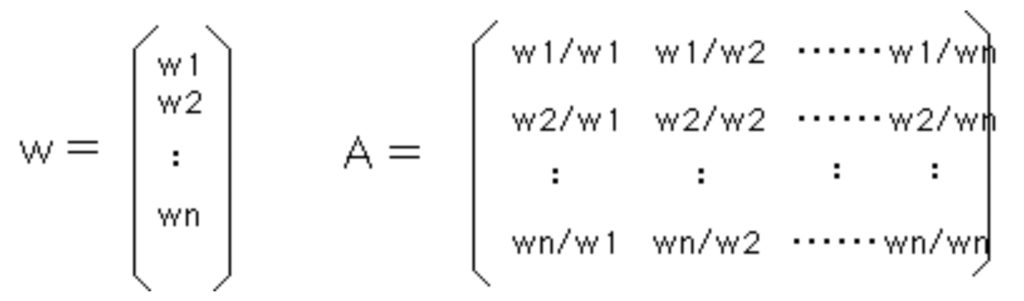
この時、AとWの積を取るとWのn倍になります。
A・W=nW
従って、(AーnI)・W=0 但し、Iは単位行列
Wが0でないためには、AーnI=0が解を持つ必要があります。従って、Aの固有ベクトルを求めることになります。そして、一対比較をしたものが、完全に整合が取れていれば、唯一の固有ベクトルを持ちますが、実際には完全に整合することは少ないので、これらの情報から整合度を求めることになります。
上の説明を読みながらリストを見れば、Mathematicaで計算している内容がよく分かるでしょう。
3.3 実際の使用例
具体的な使用例として購入したいパソコンを選ぶという意志決定問題を考えてみましょう。
この時の手順は、次の様になるのではないでしょうか。
(1)パソコンのパフォーマンスを決める要因を決める。
(2)要因間の重みづけを決める。
(3)選定したい機種毎に、各要因の点数を決める。
(4)選定したい機種毎のパフォーマンスを示す指標を計算する。
この手順の中で問題となるのは、要因間の重み付けをどうするのか、つまり、どの要因をどのくらい重視するかということです。100点満点として単純にそれぞれ25点とするのもいいし、30:30:20:20でも良いでしょうが、AHPを使えば自分の考えを正確に反映することができます。
まず、全体的なパフォーマンスを決める要因として、次の4つを考えてみましょう。
1、性能 ・・・CPU+FPUの能力等
2、使いやすさ・・・インターフェイス
3、ソフトの量・・・流通するソフトの本数
4、拡張性 ・・・周辺機器の数と性能等
次に問題となる要因間の重み付けをAHPによって算定してみた一例を示します。表の行列(筆者の意見)をAHPで算定すると(リスト3参照)、それぞれの重みは、26:56:6:12(100点満点)となります。
なお、リスト3は、リスト2を1つのプログラム(関数)としてまとめたものです。
表5:要因間の重みの比較
| 性能 | 使いやすさ | ソフトの量 | 拡張性 | |
| 性能 | 1 | 1/3 | 5 | 3 |
| 使いやすさ | 3 | 1 | 7 | 5 |
| ソフトの量 | 1/5 | 1/7 | 1 | 1/3 |
| 拡張性 | 1/3 | 1/5 | 3 | 1 |
<<リスト3>>
ahp[ahpdata_]:=
Module[{n,lmax,weightvecter,weight,ci,cr,
rcoef={0,0,.58,.9,1.12,1.24,1.32,1.41,1.45,1.19,1.51,1.53}},
n = Length[ahpdata];
If[MatrixQ[ ahpdata, NumberQ ],
,Print[“行列の入力ミスです“];Abort[]];(*入力のチェック*)
lmax=First[Eigenvalues[N[ahpdata]]];(*最大固有値*)
weightvecter=First[Eigenvectors[N[ahpdata]]];(*最大固有ベクトル*)
weight=weightvecter/Apply[Plus,weightvecter];(*要因の重み*)
Print[“要因の重み“,weight];
ci = ( lmax – n)/(n-1);(*整合度*)
Print[“整合度“,ci];
cr = ci/rcoef[[n]];(*整合比*)
Print[“整合比“,cr]]
ahpdata = {{1,1/3,5,3},{3,1,7,5},{1/5,1/7,1,1/3},{1/3,1/5,3,1}};
ahp[ahpdata]
要因の重み{0.262201, 0.565009, 0.0552855, 0.117504}
整合度0.0389941
整合比0.0433268
表6に、この要因についてPC-9801,IBM-PC(互換機)、Macintoshの標準機3種について一般的な意味で点数(10点満点)を付けたものを示します。
表6:全体的パフォーマンスの要因
| 性能 | 使いやすさ | ソフトの量 | 拡張性 | |
| PC-9801 | 5 | 3 | 7 | 7 |
| IBM-PC | 7 | 5 | 3 | 7 |
| Macintosh | 5 | 7 | 5 | 7 |
それぞれの点数と重みを掛けて足した全体的なパフォーマンスを表わす点数は、PC-9801、IBM-PC、Macintoshの順に424:564:636(千点満点)です。この程度のことは表計算でも出来ですが、Mathematicaでは逆行列を正確に計算できます(リスト4参照)。
<<リスト4>>
w={26, 56, 6, 12};(*要因の重み100点満点*)
m={{5,3,7,7},{7,5,3,7},{5,7,5,7}};(*全体的パフォマンスの点数10点満点*)
m .w
{424, 564, 636}
なお、価格を要因にいれていませんが、これは全体的パフォーマンスと価格が、比例する事が多いからです。従って、価格については、上で求めた全体的パフォーマンスを価格で割ることにより求めた価格性能比(コスト・パフォーマンス)という形で、考慮することが一般的です。
3.4 要因数が多い場合の方法
AHPの要因数は4以上13未満、できれば8未満が良いと言われています。これは、人間の同時に把握できる要因数は7つまでなどと言われるようにあまり多くの要因間の関連を考えると矛盾が生じ、一対比較を行なう際に全体的なスケールを考えながら行なえないためと言われています。従って、多数の要因を取り扱う場合には、図2に示すように要因をグループ分けし、要因を階層的に取り扱えば良いでしょう。全体のなかにおける小要因の重み付けは、その小要因が属す大要因の重みと小要因の重みを乗じた物を使用すればよいわけです。
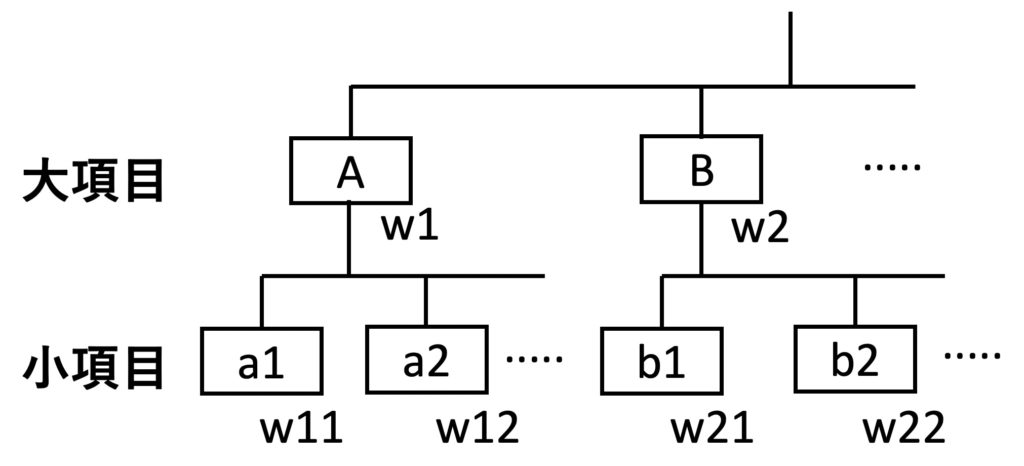
図2:要因の階層
先程のパソコンの選定を例に実際の場合のやり方を示してみましょう。パフォーマンスを決める要因を大きく4つとして考えましたが、これを更に細かく挙げるとMIPS数、FLOPS数、キャッシュメモリの大きさ、バスの転送速度、当初の起動時間、インターフェイスの形式、マウスの使いやすさ、質問できる人の数、流通ソフトの本数、PDSの数、周辺機器の数と種類、拡張スロットルの数等など色々のものが考えられます。
これらを要因と考え、AHPで重みづけを算定すればいいのでしょうが、上で述べたように要因数の制約から一度には算定できないので、要因を階層的にまとめることを考えます。上で挙げたものが全ての要因であるとはいえませんが、一例として要因をまとめると表7のようになります。
表7:パソコン選定で考えられる項目
| 大要因 | 小要因 |
| 性 能 | MIPS数FLOPS数キャッシュメモリの大きさバスの転送速度 |
| 使いやすさ | 当初の起動時間インターフェイスの形式マウスの使いやすさ質問できる人の数 |
| ソフトの量 | 流通ソフトの本数PDSの数 |
| 拡張性 | 周辺機器の数と種類拡張スロットルの数 |
性能という要因の下に、4つの小要因があるという階層的な構造となります。この4つの小要因について再度、AHPを実施して、それぞれの小要因の重みづけを算定することができます。例えば4つの要因についての重みづけが、MIPS数、FLOPS数、キャッシュメモリの大きさ、バスの転送速度の順に、0.3:0.4:0.1:0.2になったとすると全体に対するそれぞれの小要因の重みづけは、性能の要因が0.26であることから積を取って、0.078:0.104:0.026:0.052の重みづけになります。
使いやすさ、ソフトの量、拡張性の大要因についても、それぞれの小要因ごとに重みづけを算定し、同様に積を取ればよいわけです。
4 DEMATEL法
AHPは個人の感覚を数量化しようという試みでしたが、この節で述べるDEMATEL法は、次の様な考えから問題の構造を明らかにしようとする試みです。
「我々がぶつかる問題には、多くの人が共通で問題視していながら、様々な利害や考え方の対立が絡み合っており、サブ問題に分けて考えただけでは解決できないようなものもある。このような場合には、問題の客観的な分析を行なうよりも、さまざまな人々が抱いている問題意識を目に見える構造に表示すれば、対立点や価値観の差が明白になり解決に一歩でも近づくのではないでしょうか。」
このような問題の解決のために考えられたものが、DEMATEL法です。この手法が開発されることになったDEMATELプロジェクトについて次に述べます。
4.1 DEMATELプロジェクトの概要
このプロジェクトは、1982年にスイスのバテル研究所において米カンサス州立大学のファン及びティルマン教授が主体となり、実施されたものです。この目的は、現在世界中の人々が共通に悩んでいながら有効な解答が得られていない問題(これを世界的複合問題と呼びます)の構造を解明することにありました。世界的複合問題の要素項目として48個のサブ問題を選び、これをアンケートとして、世界の主要国の首脳やオピニオンリーダーと目される人々に送って一対比較を行なってもらいました。そのアンケートから得られた解答を分析評価して、その構造及び対立点を明らかにしました。
その後、両教授は米国防省の依頼により、「グローバル対ソ戦略」についての研究を行ない。DEMATELで用いた手法を発展させ、数量化の手法として完成させました。そして、それらの成果は、1989年のINF(中距離核戦力)交渉の際、使用されたと言われています。
4.2 DEMATEL法の理論と視覚化の方法
(1)影響マトリクス
アンケートの段階で図3のような影響マトリクス(M)を作成します。この影響マトリクス(M)は左第1列が影響要因、上第1行が被影響要因を表し、影響要因も被影響要因も同じものです。アンケートの段階で、その他の行、列には影響要因が被影響要因に対し及ぼす影響の程度により、0〜2を記入します(理論的には、正数であればどんな数でもよいが、記入の容易さから3段階(0〜2)又は4段階(0〜3)程度で記入するのが便利です。この際、間接的関係は考慮せず、直接的関係のみで考えます。さらに、ある要素のそれ自身に対する影響度はないとします、即ち対角要素は、0です。

図3:影響マトリクス
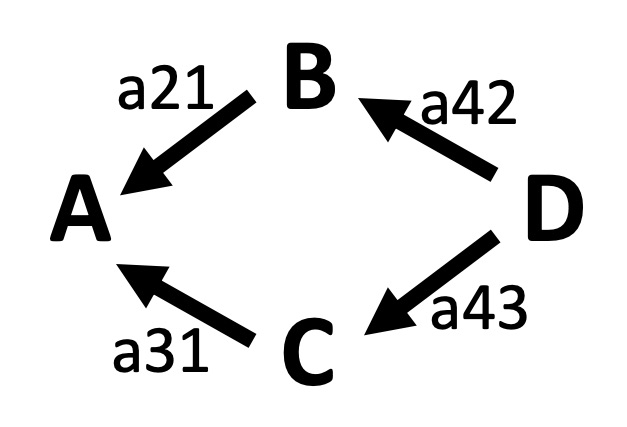
図4:間接的な影響
(2)計算の内容
この影響マトリクス(M)の行と列で加算したものを考えます。この時、行を加算したものは、その行の項目が及ぼす影響の大きさ(D:Dispater 発信という)を、列を加算したものは、その列の項目が受ける影響の大きさ(R:Recieve受信という)を表しています。但し、これは直接的な影響のみです。
間接的な影響については、影響マトリクス(M)の積を取ることで作ることができます。例えば、2次的な影響の大きさは次のように考えます。図4に示す関係では、DがAに対してB、Cを通して及ぼす2次的な影響の大きさは、a42×a21+a43×a31で示されます。これは、影響マトリクス(M)の2乗のD=>Aの要素a41×0+a42×a21+a43×a31+0×a41と同じです。つまり、Mの2乗のマトリクス(M×2)は、2次的な関係(ABC)の大きさを示します。同様に、Mの3乗のマトリクス(M×3)は、3次的な関係(ABCD)の大きさを示します。
従って、間接的な影響を含めた影響の大きさは、
M*=M+M×2+M×3+….+M×(N)+….=M(I−M)-1
により求めることができます。以後、M*を関係マトリクスと呼びます。この関係マトリクス(M*)の行、列について、それぞれ加算したもの(D*,R*)は間接的な影響を含めた項目の影響を及ぼす大きさ(発信)、及び影響を受ける大きさ(受信)を示します。
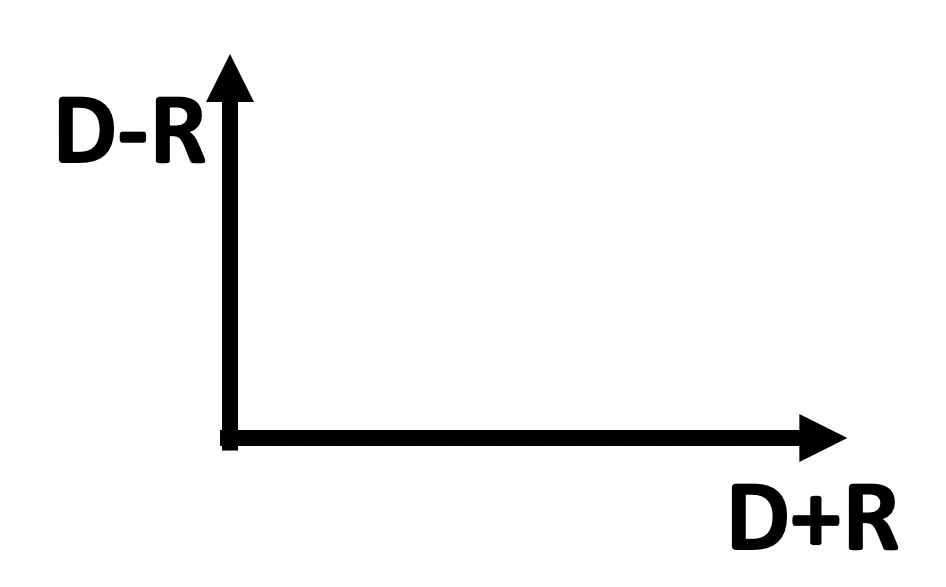
図5:要因関連図の座標軸の説明
(3)視覚化の方法
関係マトリクス(M*)を元に視覚化を行なう。この際、図5のように水平軸をD*+R*、垂直軸をD*—R*に取ります。水平軸(D*+R*)は、その項目の活性の高さを示します。つまり、D*+R*が大と言うことは影響、被影響の程度が共に大きく、重要な項目であることを示します。垂直軸(D*—R*)は、影響、被影響の差を示します。つまり、D*—R*が正ということは、発信が受信より大です。
同様に D*—R*=0….. D*=R*,
D*—R*<0….. D*<R* です。
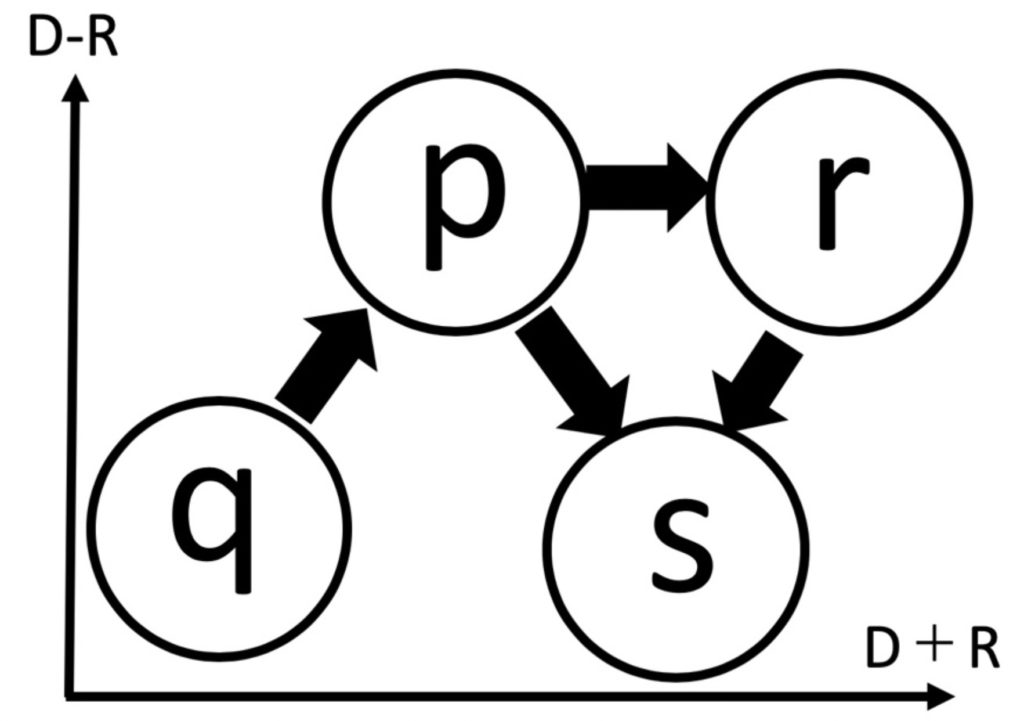
図6:要因関連図の説明
通常の場合、起こりやすい領域とその意味づけを図6に示しました。ここでs領域の項目は受信が大で発信が少ないことから、最終的な問題と考えられます。また、r領域の項目は、受信も発信も大であることから最も重要な項目です。p領域の項目は、発信が大であり、根本的な項目であると思われます。また、q領域の項目は、受信も発信も少であることから重要度の低い項目です。
さらに、ある項目からある項目への影響を矢印として表示することにより、項目間の関係を見ることができます。
4.4 DEMATEL法の使用例
生活の満足度に影響を及ぼす諸問題間の構造をDEMATEL法により明らかにしてみましょう。生活の満足度に影響を及ぼす諸問題として次の様なサブ問題を挙げてみます。
1 生活環境問題
(1)住居
(2)安全さ
2 時間の自由さの問題
(1)通勤
(2)週末
3 人間関係の問題
(1)家族
(2)近所
(3)仕事関係
4 生きがいの問題
(1)仕事
(2)趣味
5 欲望の満足度の問題
(1)金銭
(2)地位
(3)その他(食欲、性欲)
6 将来に対する不安の問題
(1)健康
(2)仕事等
(3)国の安定度(経済、政治、安全保障)
一対比較により影響行列を作れば、表8のようになります。なお、上で示されている番号は、項目の番号を示しています。
表8:生活の満足度の影響マトリクス
| 影響あれば大(3)小(1)無(0) | 生活へ | 環境へ | 時間へ | 人間関係へ | 生きがいへ | 欲望へ | 将来へ |
| 生活の満足問題が | 0 | 0 | 0 | 3 | 3 | 1 | 0 |
| 生活環境問題が | 2 | 0 | 2 | 2 | 1 | 0 | 0 |
| 時間の自由さの問題が | 2 | 0 | 0 | 2 | 2 | 1 | 0 |
| 人間関係の問題が | 3 | 1 | 1 | 0 | 2 | 0 | 2 |
| 生きがいの問題が | 3 | 1 | 2 | 1 | 0 | 1 | 1 |
| 欲望の満足度の問題が | 2 | 1 | 1 | 1 | 1 | 0 | 0 |
| 将来に対する不安の問題が | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
上の影響行列をリスト5により算定します。
<<リスト5>>
dematel[m_, noarrow_] :=
Module[{rot30, counterrot30, longness, arrow, n, maxcol, maxarrow, m1, m2, m3, m4, m5, r, d, xy, abc, xab, xv, yv, g1, g2, arrowlength},(*変数の宣言*)
rot30 = N[RotationMatrix[11 Pi/12]];(*回転*)
counterrot30 = N[RotationMatrix[-11 Pi/12]];(*逆回転*)
longness[{x_, y_}] := Sqrt[x*x + y*y];(*長さ*)
arrow[{{x0_, y0_}, {x1_, y1_}}, arrowlength_] := Block[{p1, p2, endpoint, startpoint, unitvecter},
startpoint = {x0, y0};
endpoint = {x1, y1};
unitvecter = (endpoint – startpoint)/ longness[endpoint – startpoint];
p1 = endpoint + (rot30.unitvecter)*arrowlength;
p2 = endpoint + (counterrot30.unitvecter)*arrowlength;
{Line[{startpoint, endpoint}], Line[{p1, endpoint, p2}]}];(*矢印*)
If[MatrixQ[m, NumberQ], , Print[“行列の入力ミスです”]; Abort[]];(*入力のチェック*)
n = Length[m];(*行列のランク*)
maxcol = Max[m.Table[1, {i, n}]];(*行の和の最大値*)
maxarrow = n (n – 1);(*矢印の最大数*)
If[noarrow > maxarrow, Print[“矢印の数が多すぎます!!”]; Abort[],];
m1 = m/maxcol;(*影響行列に尺度係数を乗ずる*)
m2 = N[m1.Inverse[IdentityMatrix[n] – m1]];(*関係行列の作成*)
m3 = Module[{a = {}}, Do[If[i == j, , AppendTo[a, {i, j, m2[[i]][[j]]}]], {i, 1, n}, {j, 1, n}];
a];(*項目間の関係度*)
m4 = Sort[m3, (#2[[3]] < #1[[3]]) &];(*関係の大きな要素のソート*)
Print[“関係の大きい順に並べた要素番号”, Table[m4[[i]], {i, noarrow}]];
r = Apply[Plus, m2];(*他に及ぼす影響の大きさ*)
d = Apply[Plus, Transpose[m2]];(*他から受ける影響の大きさ*)
xy = N[Transpose[{r + d, d – r}]];(*要因関連図の座標の計算*)
m5 = Table[{xy[[m4[[i]][[1]]]], xy[[m4[[i]][[2]]]]}, {i, noarrow}];(*矢印の作図データ*)
{xv, yv} = Transpose[xy];
arrowlength = Max[Max[xv] – Min[xv], Max[yv] – Min[yv]]/15;(*矢印の長さ*)
abc = Table[i, {i, n}];(*番号*)
xab = Transpose[{abc, Transpose[Transpose[xy] + {arrowlength/2, 0}]}];(*番号の位置データ*)
displaytext[{a_, b_}] := Text[a, b];(*テキストの作図*)
g1 = ListPlot[xy];(*点の作図*)
g2 := Graphics[{Map[displaytext, xab]}];(*番号の作図データ*)
g3 := Graphics[Map[arrow[#, arrowlength] &, m5]];(*矢印の作図データ*)
Show[g1, g2];(*番号の作図*)
Show[g1, g2, g3](*矢印の作図*)]
m={{0,0,0,3,3,1,0},{2,0,2,2,1,0,0},{2,0,0,2,2,1,0},
{3,1,1,0,2,0,2},{3,1,2,1,0,1,1},{2,1,1,1,1,0,0},{1,0,0,0,1,0,0}};
dematel[m,10](*計算の実行*)
<<出力結果>>
関係の大きい順に並べた要素番号
{{5, 1, 1.33105}, {4, 1, 1.28949}, {3, 1, 1.13214}, {2, 1, 1.12664}, {1, 5, 1.09462}, {4, 5, 1.08372}, {3, 5, 1.00235}, {1, 4, 0.989085}, {6, 1, 0.982747}, {5, 4, 0.936719}}
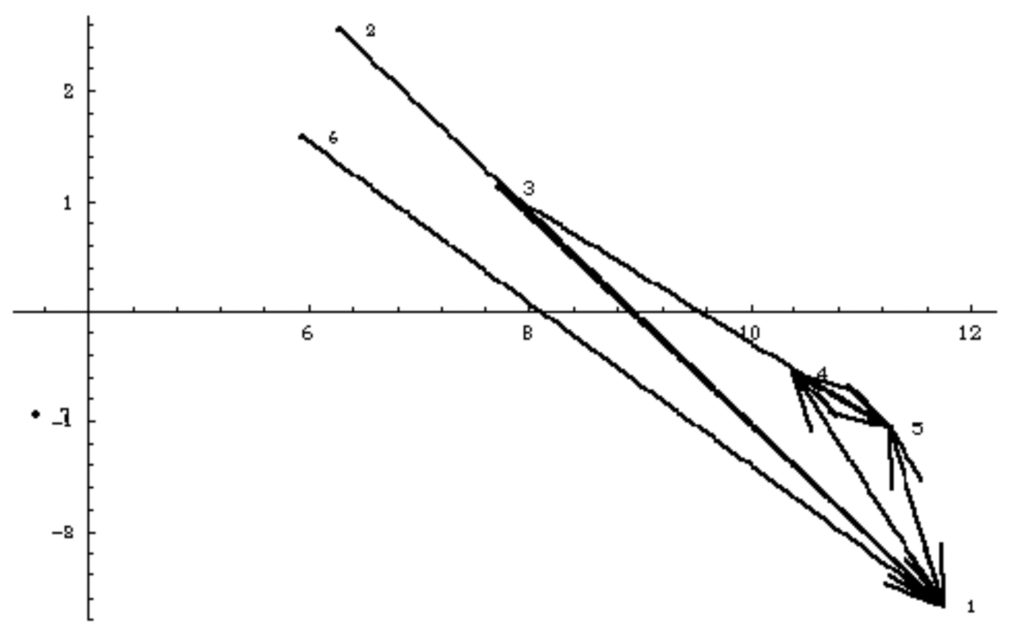
図7:問題の関係図
図7を簡単に解釈すると生活の満足問題に対して、将来に対する不安以外はそれぞれ関連していると考えています。その中でも最も重要なサブ問題は人間関係と生きがいの問題であり、それらに大きな影響を与えているものとして時間の自由さの問題と考えています。
4.5 解析実施の際の留意事項
1 項目の選択
問題を十分に分析することは、非常に重要です。さらに、項目の挙げ方で思考の範囲が決まってしまうので、項目の選定には十二分に時間を掛け、推敲をする必要があります。
(1)項目の列挙
項目を挙げる方法には次の2つがあります。
ア 関連する項目を挙げる場合
対象としている問題に関連の有ると思われる項目を整理して列挙する。表1に例題について挙げた項目の一例を挙げます。通常、表1にあるように項目を階層的に列挙しますが、項目は考えられるだけ挙げます。そして、対象とする問題と範囲及び項目数を考えて、どの階層の項目を関連する項目として挙げるかを決めます。また、関連する項目だけでは問題との関係が分からないので、最終的な影響の及ぼされる項目として問題となる項目を入れておく必要があります。
イ サブ問題を挙げる場合
対象としている問題が多くのサブ問題の有機的なかかわりによるものである場合には、それらのサブ問題の関連を明らかにすることが問題解決の1つの方法です。この時、サブ問題間の関連は考えずにブレーンストーム的に色々なものを挙げた後、整理統合することが大切です。
(2)項目の整理
ある程度、項目を整理して、30個以下の要素数になったならば、まず1度、試しにDEMATEL法を実施してみます。それによって、抜けている要素に気づくことも多いし、また、グラフ化してみると余り重要でない要素が分かるので、さらに整理するのに役立ちます。
特にアンケートを実施する場合、記入する人と要素選択者とが別なので選択には十分注意しなければなリません。ここではあまり一般的でも、あまり専門的でもないこと、また、改善案は、容易に思い付くが、価値観の差が出るような項目を選ぶ方が、相異点が明確に成りやすいでしょう。さらに、要因の項目数は記入の手間を考えると20個程度に留めた方が良いでしょう。
(3)項目の定義の明文化
要因の内容について、明文化しておくと後の解釈の段階で役立ちます。特にグループにおけるコンセンサスを得るためにDEMATEL法を実施する場合には、問題に関連する要因を、ブレーンストーミングにより列挙する際、要因の内容について、明文化しておくと良いでしょう。
2 図の解釈
(1)解釈
視角化の方法で説明したように項目の存在する領域と項目の意味を考えて項目間の全体的な関連を解釈する必要があります。その際、重要である、または、ないと考えている項目や問題点に大きく影響を与えている項目に注目して解釈すると良いでしょう。
(2)類型化
複数の影響マトリクスについてグラフ化及び解釈を行なった後、キーワード、重要でないと考えている項目及び全体的な形などに注目して類型化を行ないます。特にグループにおけるコンセンサスを得るためにDEMATEL法を実施する場合には、2〜3の形に類型化し、どれにも該当しないものは無理に類型化することなく、その他とするのが良いでしょう。
4.6 DEMATEL法の別の使用例
4.3に示した生活の満足度に関する構造を明らかにする問題以外に別のタイプの問題を挙げて、DEMATEL法の可能性を例示します。
仮説として「国の間の経済的な影響関係は、貿易額で示される。」というものを考え、DEMATEL法により貿易額による経済的な関係を明らかにしてみましょう。
日本との貿易の多い5地域・国の2018年の相互の貿易額を示したものが、表9です。これをDEMATEL法により、経済関係を明らかにした結果が図8です。なお、資料では東アジアとして中国、台湾、韓国及びASEANを累計したものをあげていましたが、台湾、韓国に分離しました。また、地域内での貿易はあるのですが、関係行列として対角行列は0と仮定しました。
表9:国家間貿易の例(2018年、百万ドル)
| 輸出輸入 | 日本 | 米国 | 中国 | EU | 台湾・韓国 | ASEAN |
| 日本 | 0 | 74,967 | 147,565 | 76,206 | 167,263 | 117,334 |
| 米国 | 140,664 | 0 | 480,689 | 480,469 | 110,776 | 161,404 |
| 中国 | 144,053 | 120,341 | 0 | 247,568 | 250,253 | 202,230 |
| EU | 83,740 | 319,654 | 411,943 | 0 | 85,517 | 164,557 |
| 台湾・韓国 | 352,659 | 295,646 | 482,050 | 446,946 | 0 | 641,144 |
| ASEAN | 114,476 | 86,204 | 321,785 | 114,420 | 155,198 | 0 |
※ジェトロ世界貿易投資報告 2019年版参照。対角行列は0とした。
<<リスト6>>
m = {{0, 74967, 147565, 76206, 167263, 117334}, {140664, 0, 480689,
480469, 110776, 161404}, {144053, 120341, 0, 247568, 250253,
202230}, {83740, 319654, 411943, 0, 85517, 164557}, {352659,
295646, 482050, 446946, 0, 641144}, {11447, 686204, 321785,
114420, 155198, 0}};
dematel[m, 10] (*計算の実行*)
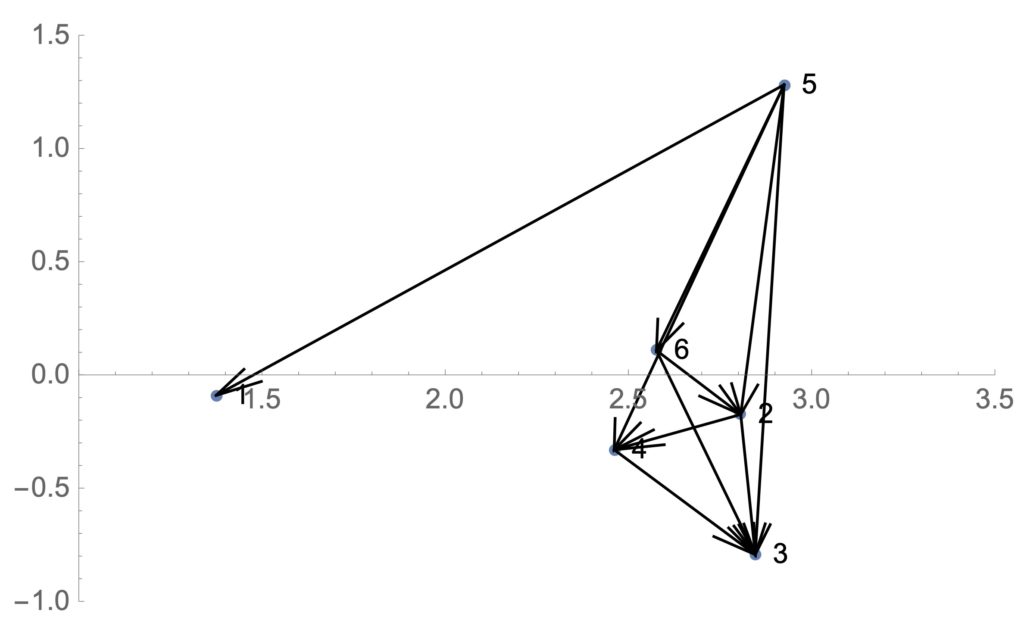
図8:地域・国家間貿易による経済関係
図8では、1が日本、2が米国、3が中国を示しています。1990年代には今回の5の位置にいた日本ですが、変化等がよく捉えられていると思います。その他の例としては、メールのやり取りを解析して送受のメール数から人間関係を相互に与える影響度により解析する等が考えられます。
参考文献
AHPについての入門書
1 刀根 薫 「ゲーム感覚意志決定法 –AHP 入門 –」日科技連
DEMATEL を含む各種意志決定理論の入門書
2 木下栄蔵 「意志決定論入門」啓学出版
3 中村健蔵2019『MathematicaによるOR』楽天Kobo・キンドルDP
ノートブックのダウンロードについて
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。