要旨:パッチワーク の繋がりやデザインを考える上で重要なタイリングについて具体例を挙げて説明しています。
1.1 タイリングの導入
キルトのデザインを考えるときの基本は図1正方形タイリングです。これを眺めてデザインを考えても同じ様なデザインしか出てこないと思っている方は幾何学の視点からヒントを出来るだけ判りやすく解説するので、参考にしてください。なお、決して数式や証明などは出てこないので、気軽に読んでいただけるものになっています。

図1:正方形タイリング
ところで、タイリングという言葉が気になっている方もいらっしゃるかもしれません。タイルリングは、タイル、つまり、ある形の平面図形で平面を隙間なく埋めることをいいます。日本の数学用語では平面充填という硬い用語ですが、英語ではTilingとイメージしやすい用語なので、こちらを用い、タイリングとカタカナ表記することとしました。

図2:正多角形タイリング(正三角形、正六角形)
なお、1種類で同じ大きさの正多角形によるタイリングには、先ほどの図1正方形の他に図2 正三角形と正六角形があることはご存知の通りです。
1.2 正方形タイリング
それでは、多くの方が取り組んでいる正方形タイリングについてもう少し詳しく見ていくことにします。
さて、同じ大きさの正方形タイリングであれば、変化をつけようとすると図3の様に、縦もしくは横方向のどちらかにずらしていくことしかできません。
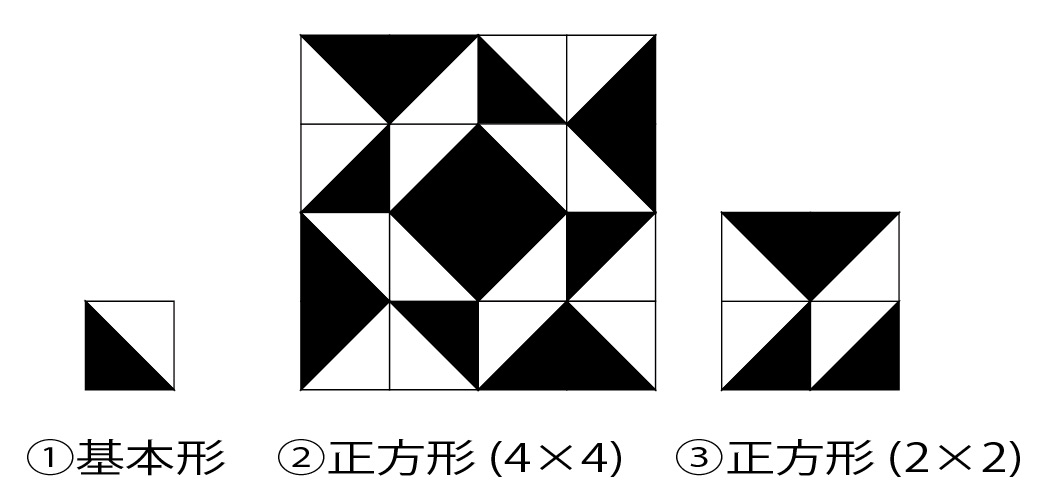
図3:正方形タイリングの変形(縦横のどちらかへ、水平に半分ずらした例)

図4:大きさ2種の正方形デザイン

図5:大きさ3種の正方形タイリングの一例
それでは、もっと変化をつけるために正方形の大きさが違っても良いとします。まず、2種類の大きさの正方形タイリングを図4に、3種類を図5の様に作ることができます。図4右図で1対3の大きさの正方形タイリングになっていることがわかります。図5は1対2対3の正方形タイリングで、なかなか変化のあるものができます。これと同様に大きさの種類を増やしていけば、面白いデザインになるかというとそう言うわけにも行きません。

図6:4種類以上の大きさの正方形タイリングの例
図6は、一辺112の大きな正方形を21個の小さな正方形に分割している例です。図6の数字は正方形の辺の長さです。この様に4種類以上の大きさの正方形タイリングも作ることができますが、大きさの種類を増やしていっても変化に富んで、見栄えのいいものになるというわけではありません。
さて、ここでうまい方法がないかと言うと内部分割という方法がありますので、ご紹介します。
まず、図7に示す様に正方形の内部分割といっても任意の位置で分割できるわけではありませんが、当分分割するのであれば、任意の整数で当分分割できます。
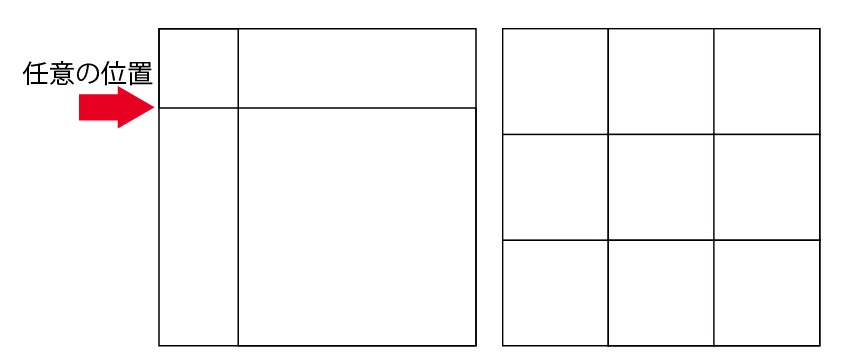
図7:正方形の内部分割(任意の位置では分割できない例、等分分割の例)
そして、図8の様にルールを決めて内部分割すれば、まとまりのある形にすることができます。さらにそれらを回転させて4つ並べてさらに大きな正方形を作ることもできます。そして、最小の正方形を基本の最小ピースだと考えれば良いわけです。図8の色付けした例では、16✖16ピースと考えることができます。
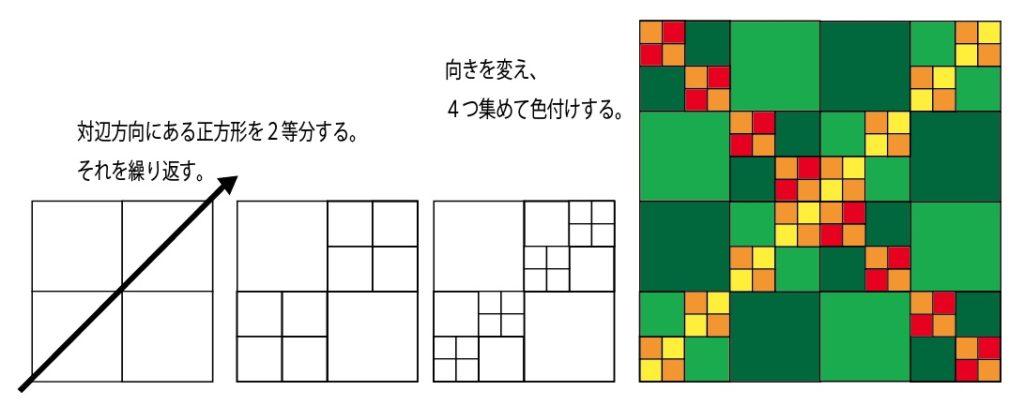
図8:正方形の内部分割の一例(2分割)
図8は2分割を3度繰り返したものですが、3分割を3度繰り返した例が図9です。こちらも3分割の規則性が目に見えて面白いデザインになっています。3分割を3度繰り返した例なので、27✖27ピースと考えることができます。

図9:正方形の内部分割の一例(3分割)
1.3 正三角形タイリングと正六角形タイリング
正三角形と正六角形がタイリングできるわけですが、結論から言うと正六角形タイリングは正三角形タイリングに集約することができます。理由は、次の図を見てください。①図10:正六角形は、正三角形を6つ集めることで作ることができます。②図10:正六角形タイリングは隙間なく内部分割することはできません。③図11:正三角形タイリングは正方形タイリングと同様に内部分割することができます。
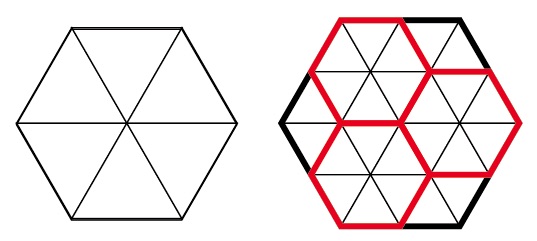
図10:正六角形と正三角形(正三角形に内部分割、正六角形だけには分割不能)
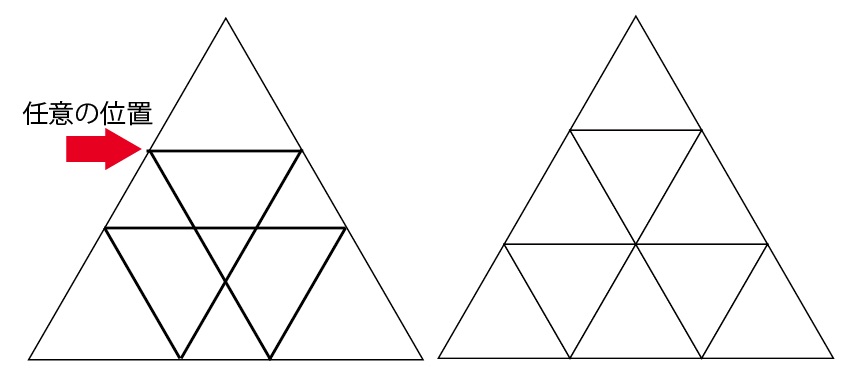
図11:正三角形の内部分割(任意の位置では分割できない例、等分分割の例)
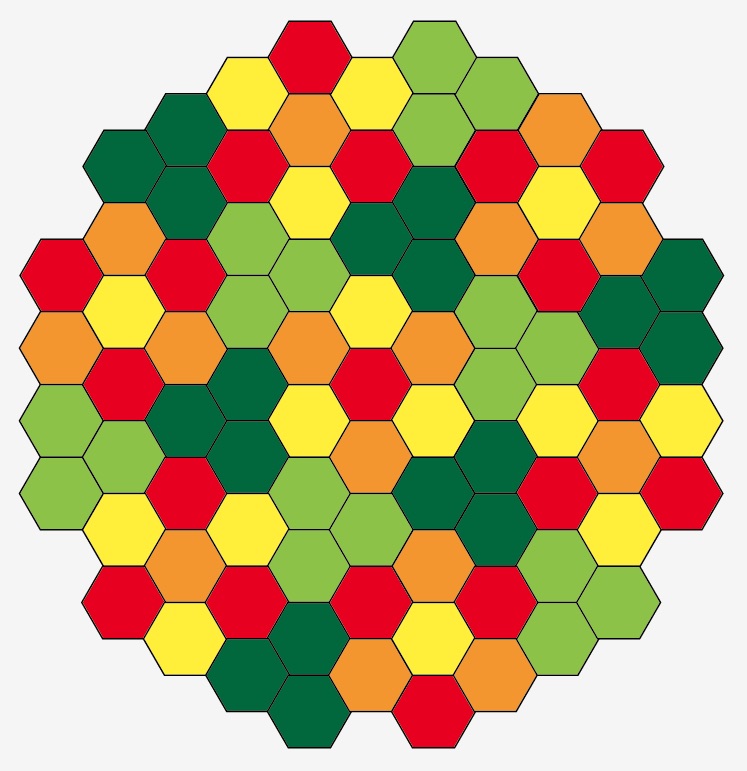
図12:正六角形タイリングによるデザインの一例
したがって、図12の様に正六角形だけでデザインを考える場合を除いては、正三角形タイリングを基本としてデザインし、6つ集めて正六角形を構成すれば良いわけです。デザインへの応用という観点からは正三角形タイリングだけを考えれば良いものと考えます。

図13:正三角形タイリングにおける内部分割の例
正三角形タイリングについては、正方形タイリングと同様に内部分割により、まとまり・規則性のあるデザインにすることができます。図13の例では、2分割して中央の正三角形以外について2分割することを3回繰り返したものです。鱗紋とも違ったインパクトのあるデザインになっています。
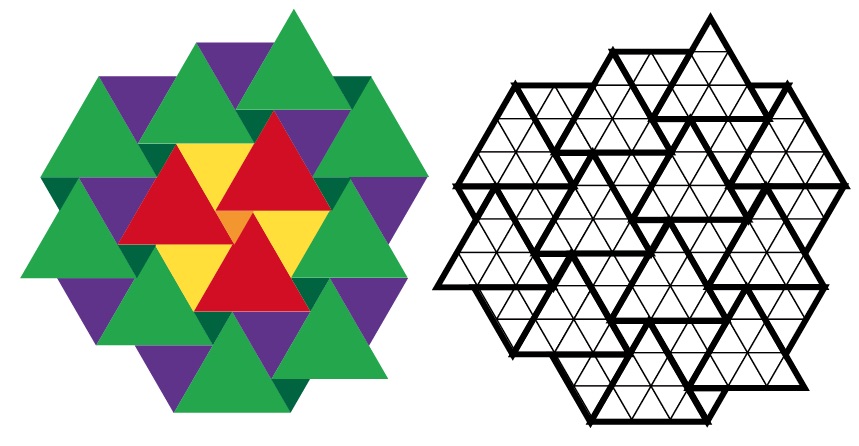
図14:大きさの違う正三角形を使ったデザイン
また、正方形タイリングと同様に大きさの違う正三角形を使ったデザインも図14の様に正三角形タイリングとして、まとめることができます。
さらに正三角形を6つ集めることで正六角形を作ることができますので、図15の様に大胆な変化をつけることもできます。

図15:正三角形タイリングによる正六角形を取り入れたデザイン
さて、幾何学の視点から最も基本となる正方形をはじめとして、1種類の正多角形によるタイリングについて解説しました。キルトデザインの何かのヒントになっていれば、嬉しい限りです。次回は2種類以上の正多角形を使ったタイリングについて解説する予定です。ご意見・ご感想を編集部までお寄せください。
参考文献
1 中村健蔵1998年「Mathematicaで絵を描こう」東京電機大学出版会
2 B.Grunbaum他 1986“Tilings and Patterns”W.H.Freeman and Company
3 中村健蔵2019『パッチワークキルターのための幾何学デザインシリーズ 幾何学で進化するキルトデザイン』楽天Kobo・キンドルDP


