概要: 1回目としてMathematicaで定義されている立体について解説し、回転させてみます。
多面体を表示する
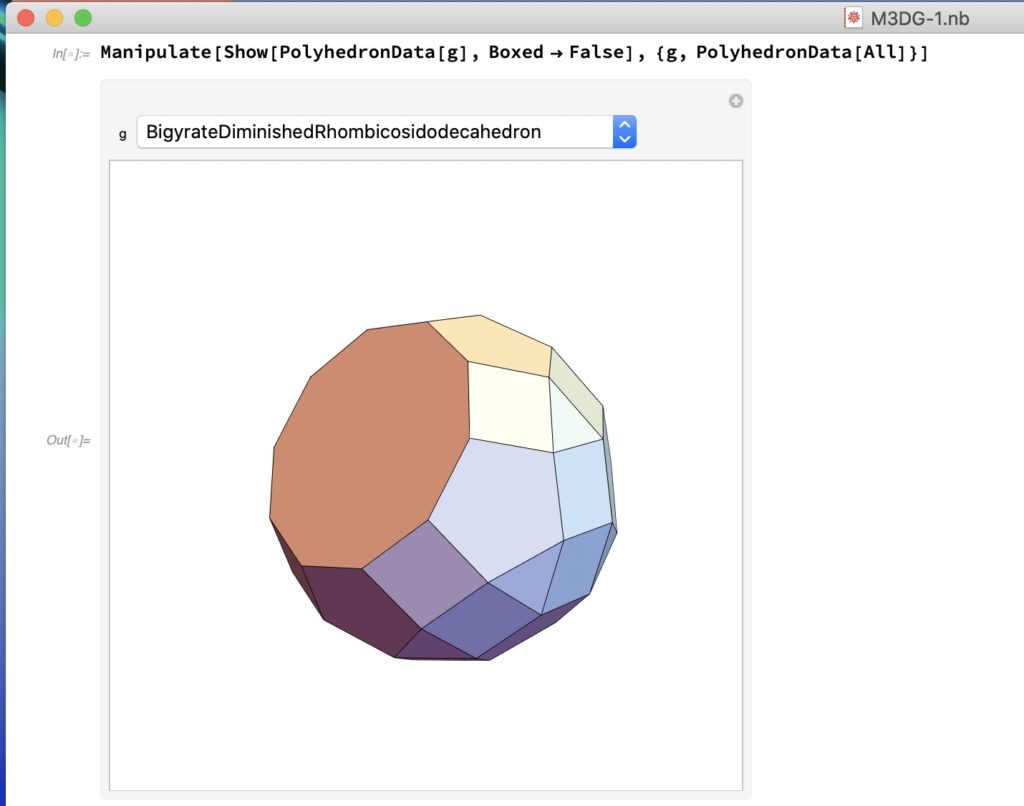
Mathematicaでは、PolyhedronDataに200種類の多面体が定義されており、専門家以外には珍しいものばかりです。表示するのはプログラム1の通りに簡単です。図1左図がその表示で、カーソルを多面体に近づけると図のような回転マークが出て、ドラッグすれば、回転させることができます。表示する多面体の種類を選ぶには、箱の上部にある多面体の名称をクリックすれば、200種類の多面体の名称が表示されるので、それを選択します。ただし、種類が多いのと英語名であることから思いのものを選ぶのは難しいかも知れません。
<<プログラム1>>
Manipulate[Show[PolyhedronData[g], Boxed -> False], {g, PolyhedronData[All]}]
図1:PolyhedronDataの表示と名称の選択
多面体については、展開図があるものはプログラム2で図2の通り表示させることができます。図1左図の多面体は、正三角形、正方形、正五角形と正10角形の面を持つもので、図2にその展開図を示しました。
<<プログラム2>>
Manipulate[PolyhedronData[g, “Net”], {g, PolyhedronData[All]}]
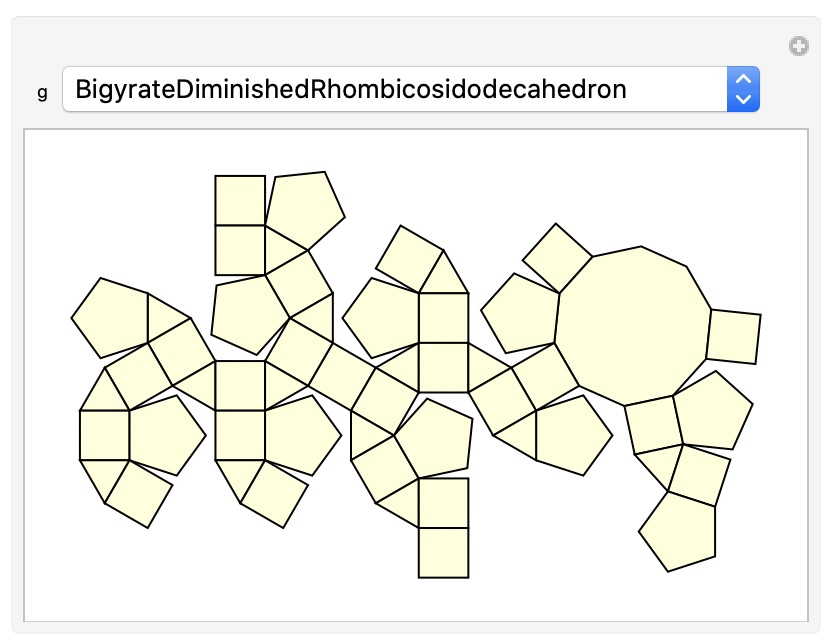
図2:展開図の一例
表示したい多面体の名称が決まれば、それだけを表示するのはプログラム3で図3の通り簡単です。ここでは“GreatStellatedDodecahedron”大星型20面体を表示した。
<<プログラム3>>
Show[PolyhedronData[“GreatStellatedDodecahedron”], Boxed -> False]
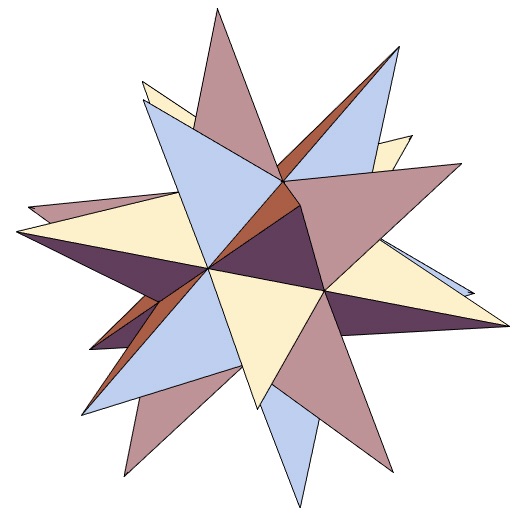
図3:大星型20面体を表示
いよいよ図3に表示した多面体を回転させることを考えよう。図4に説明図を示した。
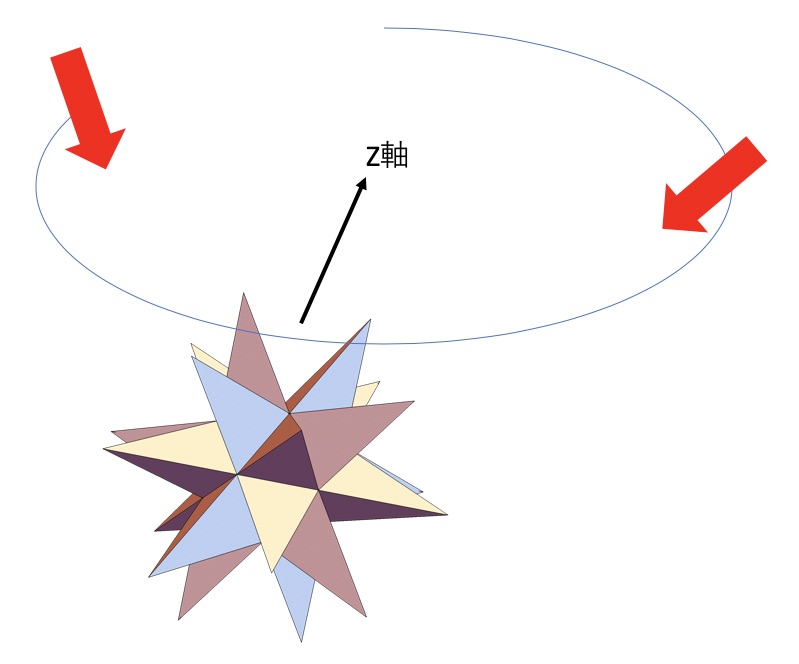
図4:多面体を回転させるため説明図
多面体が回転しているように見せるためには、図4のようにZ軸に直交する円上の点から視点を回転させれば、多面体が回転して見える。こちらの方が多面体を回転させるよりも簡単です。これをプログラムにしたものが、プログラム4で図5のように表示される。実際の動画は図6です。
<<プログラム4>>
Animate[Show[PolyhedronData[“GreatStellatedDodecahedron”],
Boxed -> False, SphericalRegion -> True, ImageSize -> 200,
ViewPoint -> 3. { Sin[t], Cos[t], 1}], {t, 0, 2 Pi, Pi/120}]
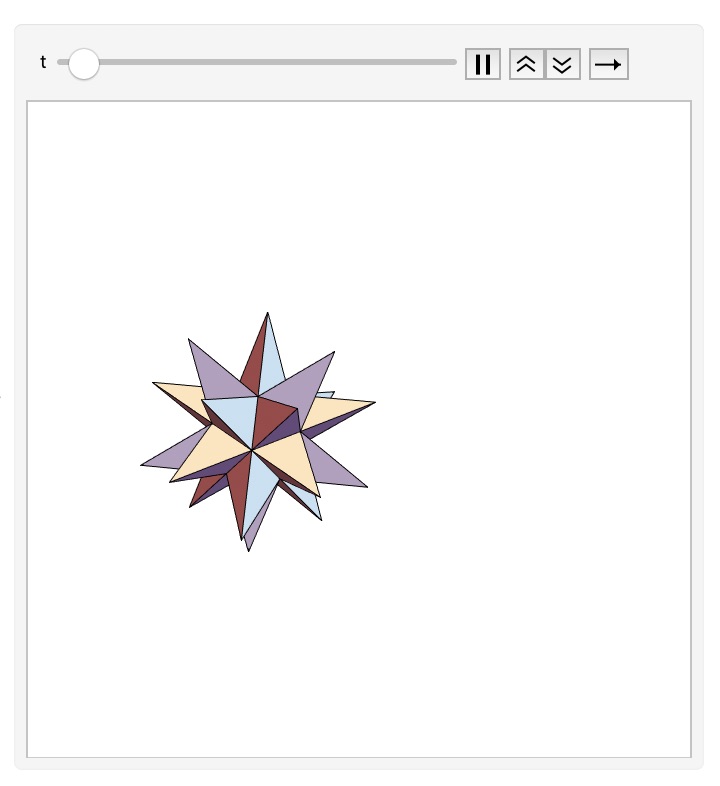
図5:プログラム4の表示:実際には箱の中で図6の動画が見られる。
図6:多面体の回転(動画)
その他の立体の解説
Mathematicaで定義されている立体には他にも色々なものがあるので表で紹介します。
表:その他の立体の説明
| データ名 | 説明 |
| SolidData | 球などの有名な数学立体:33個。特性値を求めることができる。 |
| SurfaceData | 特徴的な曲面:178個 |
| KnotData | (閉じた縄の)結び目:6個 |
| ExampleData | 試作した各種データのうちベートウベンの胸像、スペースシャトルなどの立体:27個 |
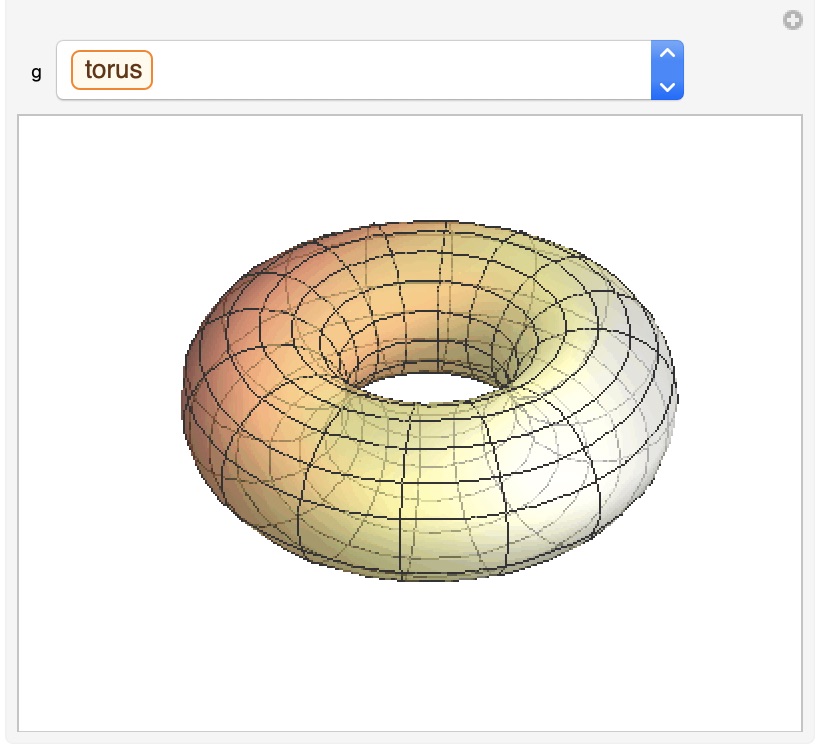
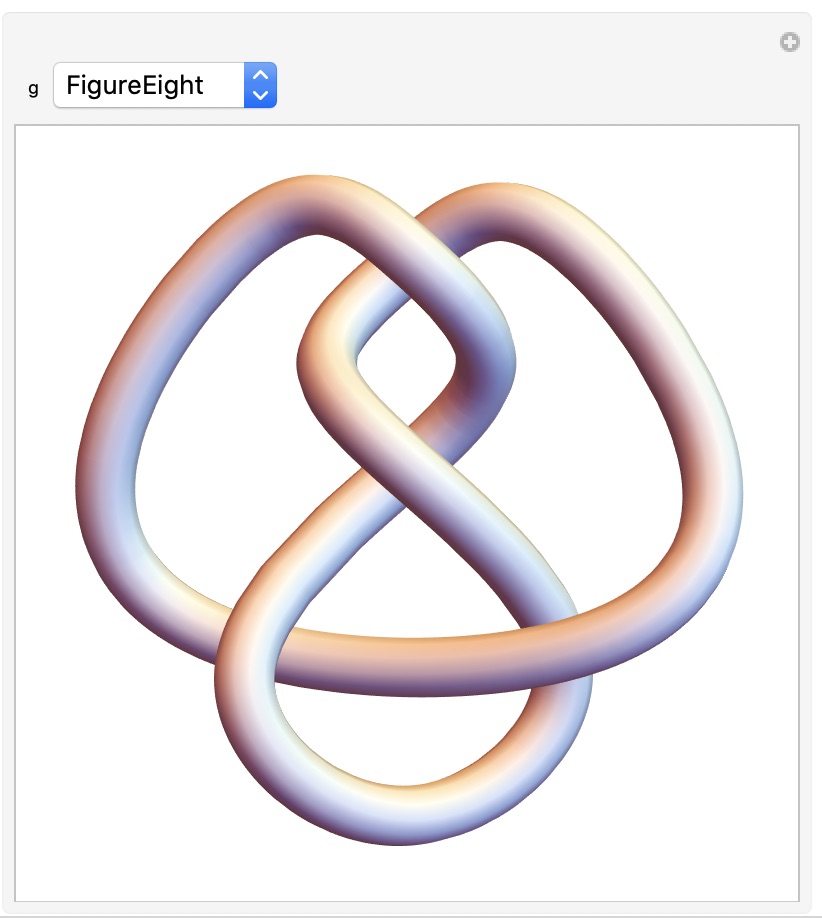
プログラム5でそれぞれのイメージを図7のように見ることができます。図7のSolidDataとSurfaceDataは同じトーラスを示していますが、SolidDataの方は光沢があり、SurfaceDataの方は半透明で経線が描かれており、違いがあります。SurfaceDataは多彩でこの曲線が数学世界でどんな役割を果たしたのか興味が湧きます。閉じた縄の結び目は思ったよりも美しいので見てください。ExampleDataは色々なものがあり、Wolfram社の多様性を表しているようです。
<<プログラム5>>
Manipulate[SolidData[g, “Image”], {g, SolidData[All]}]
Manipulate[SurfaceData[g, “Image”], {g, SurfaceData[All]}]
Manipulate[KnotData[g, “Image”], {g, KnotData[]}]
glist = Table[ExampleData[“Geometry3D”][[i]][[2]], {i,
Length[ExampleData[“Geometry3D”]]}];
Manipulate[ExampleData[{“Geometry3D”, g}], {g, glist}]
図7:その他の立体イメージ:順番にSolidData、SurfaceData、KnotData、ExampleData
立体の回転
さて、ここで紹介した立体は、プログラム4で立体名を変えるだけで回転させることができます。プログラム5では、結び目とスペースシャトルを回転させていますが、それぞれ違うところは視点のZ座標を変えています。結び目ではz=10としてずっと上から見下ろしています。スペースシャトルの方は背面の色をLightBlueにして、z=-0.2として、ちょっと下から底盤も見えるようにしました。それぞれの動画を図8、9に示します。
<<プログラム5>>
Animate[Show[KnotData[“SolomonSeal”], Boxed -> False,
SphericalRegion -> True, Background -> LightBlue,
ImageSize -> 300, ViewPoint -> 3. { Sin[t], Cos[t], 10}], {t, 0, 2 Pi, Pi/120}]
Animate[Show[ExampleData[{“Geometry3D”, “SpaceShuttle”}],
Boxed -> False, SphericalRegion -> True, Background -> LightBlue,
ImageSize -> 300, ViewPoint -> 3. { Sin[t], Cos[t], -0.2}], {t, 0, 2 Pi, Pi/120}]
図8:結び目の回転
図9:スペースシャトルの回転
以上、Mathematicaで定義されている立体について解説し、回転させてみました。既に定義されたものだけでも結構楽しめそうだと思われたことと思います。次回はアニメーションを動画として取り出す方法について解説します。
参考文献:Mathematicaグラフィックスの入門書
中村健蔵「Mathematicaで絵を描こう」1997東京電機大学出版局
ノートブックのダウンロードについて
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。