概要: 2回はMathematicaで作成した動画をファイル作成するとともにステレオ立体視の動画を作成する。
動画ファイル作成
動画ファイル作成するのは、思ったよりも簡単です。第1回のスペースシャトルの動画ファイル作成する場合をプログラム1に示しています。
<<プログラム1>>
Table[Show[ExampleData[{“Geometry3D”, “SpaceShuttle”}],
Boxed -> False, SphericalRegion -> True, Background -> LightBlue,
ImageSize -> 400, ViewPoint -> 3. { Sin[t], Cos[t], -0.2}], {t, 0, 2 Pi, Pi/600}];
Export[“SpaceShuttle.avi”, %, “FrameRate” -> 20]
プログラム1を解説します。最初の3行で画像をリストとして作成しています。これは第1回と見比べると解りますが、アニメーションを作る関数Animationをリストを作成する関数Tableに変えただけです。そして、作られた画像リストをファイルとして作成しています。4行目の%は、この関数の前の関数が作成したものを示しています。作成するファイルの名称と種類は”SpaceShuttle.avi”として指定しています。つまり、A V Iの動画ファイルを作成しています。
次に動画作成の際に考えるべき、フレームレイトと画質について説明します。画質はImageSize -> 400で指定します。この場合、400✖️400ピクセルです。フレームレイトは全体の表示時間との関係でファイルの大きさに関係してきます。この場合、スペースシャトルが360度回転するのに60秒、フレームレイト20とすると1200枚の画像を必要となります。従って、時間tを{t, 0, 2 Pi, Pi/600}としているわけです。なお、この時、作成されたA V Iファイル容量は587Mにもなります。画質を上げれば、ファイル容量も大きくなりますから画質とスムーズさは考慮されなければ、いけません。
ファイル容量が削減できる場合の方法
上の場合、ファイル容量は587Mと大きくなりましたが、ファイル容量が削減できる場合とその方法について説明します。第1回の立体の場合、上の場合と比べると5分の1にファイル容量が削減されています。秘密はプログラム2を見ていただければ、判ります。
<<プログラム2>>
Table[Show[PolyhedronData[“GreatStellatedDodecahedron”],
Boxed -> False, SphericalRegion -> True, ImageSize -> 400,
ViewPoint -> 3. { Sin[t], Cos[t], 1}], {t, 0, 2 Pi/5, Pi/120}];
Export[“GSD.avi”, %, “FrameRate” -> 20]
大星型正20面体の場合、視点の回転軸から見ると5回の対称性があります。従って、回転を360度の5分の1、つまり、72度として後は繰り返せば、回転しているように見せることができるわけです。なお、繰り返しについてWebの表示法で指定しています。
また、第1回の結び目についても5回の対称性がありますので、同じことができます。
ステレオ立体視について
これで終わっては面白くありませんから、作成した立体を立体的に見る方法を図1で説明します。
裸眼立体視とも呼ばれるもので、人間は立体を見た時に左右の目の視差を合成して立体に見えるわけです。これを応用し、視差を持つ2枚の画像を作成し、左図を左目で、右図を右目で見て、左右の目の視差を合成して立体に見ようとするものです。この場合、左右がそのままの見かたですので、平行法と呼ばれています。
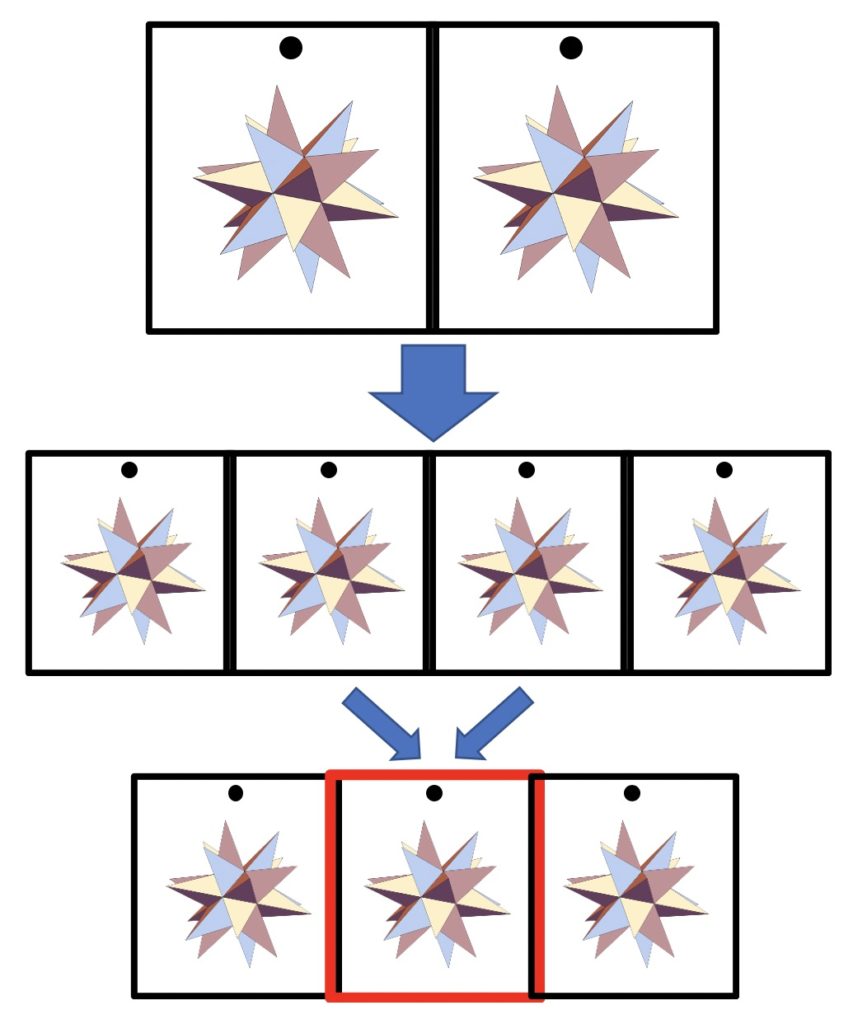
図1:ステレオ立体視(平行法)の見方
図1でステレオ立体視(平行法)の見方を説明します。立体視する図は上段の様に視差を持った2つの図が並んでいます。それを眺めていると中段のように4つの図に見えてくるので中央の2つ図を下段のように重ねると中央の図が立体に見えます。図の中央上部に黒点を描いていますが、それを重ねるようにすれば比較的簡単です。慣れないうちは目や肩が凝ったりしますので、あまり集中しないでください。慣れてくれば、ある意味では自然な動作ですから集中しなくても見れるようになります。ただし、慣れて見続けているとドライアイが心配ですから、ご注意ください。
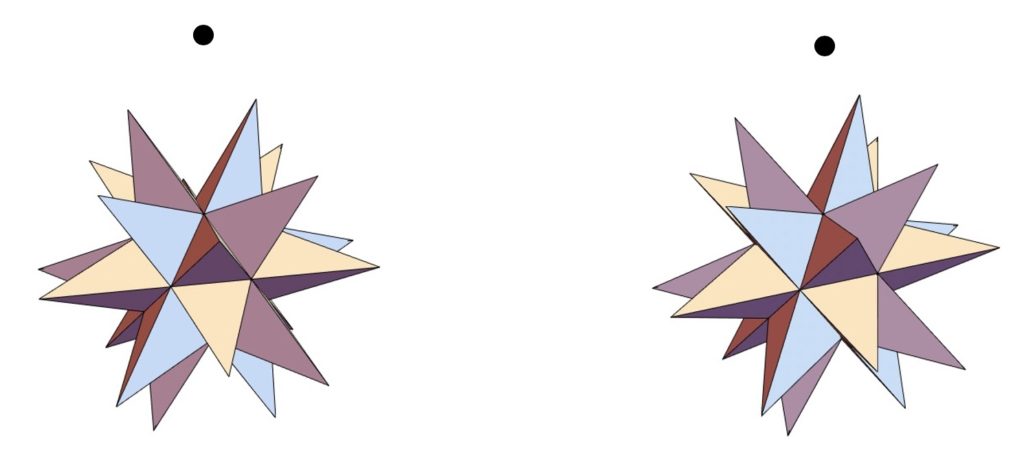
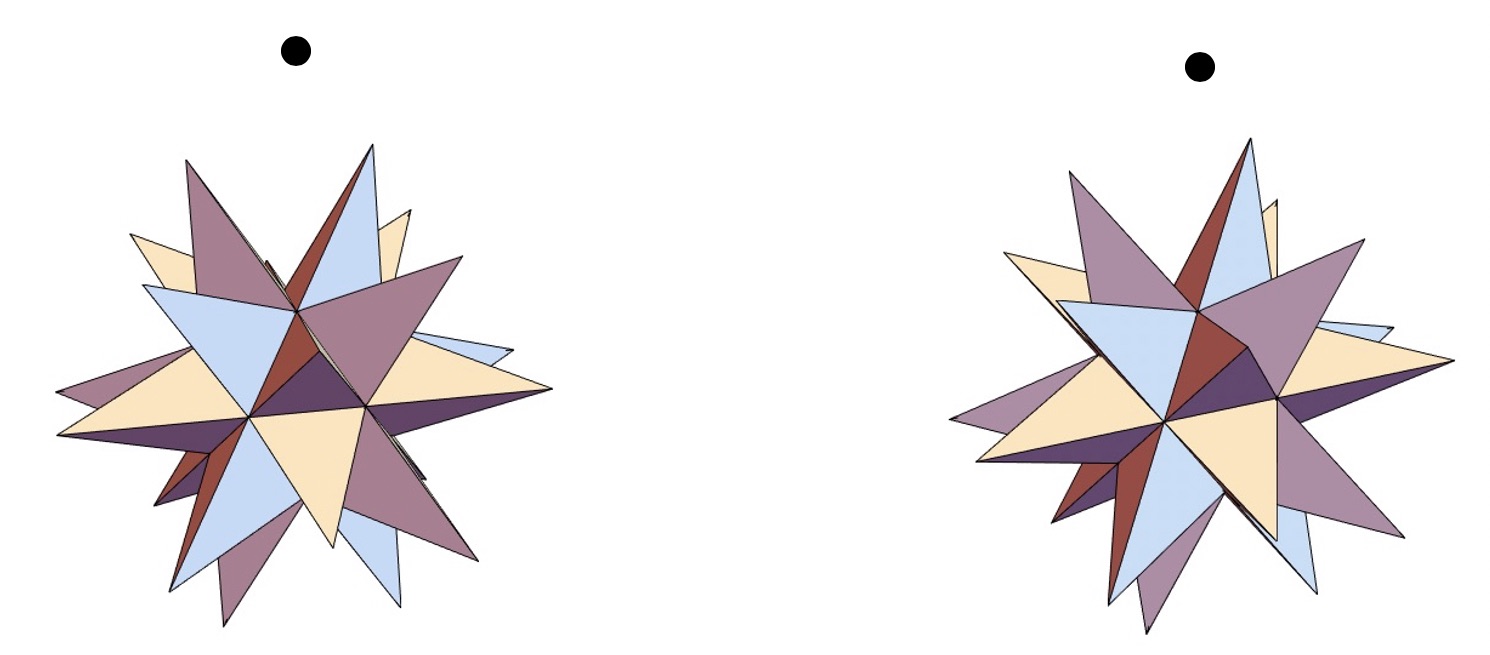
図2:ステレオ立体視(平行法)の一例
図2はステレオ立体視(平行法)の一例です。左右の立体は9度の視差を持って描かれています。9度は両手で小物を持った時に生じる視差に相当する角度で最も立体感が生まれると言われている角度です。
図2はプログラム3で描いた動画のスクリーンショットの上部中央に黒点を描き加えています。GraphicsRowについての説明は、Mathematicaグラフィックス入門6を参照して下さい。
なお、慣れないうちは図の幅を10cm以内にすると簡単に見ることができます。慣れてきても幅を15cm以上取ると目がきついので、Webページを見る時にご注意ください。
<<プログラム3>>
Animate[GraphicsRow[{Show[ExampleData[{“Geometry3D”, “SpaceShuttle”}],
Boxed -> False, SphericalRegion -> True,
Background -> LightBlue,
ImageSize -> 300, ViewPoint -> 3. { Sin[t], Cos[t], -0.2}],
Show[ExampleData[{“Geometry3D”, “SpaceShuttle”}], Boxed -> False,
SphericalRegion -> True, Background -> LightBlue,
ImageSize -> 300,
ViewPoint -> 3. { Sin[t + Pi/20], Cos[t + Pi/20], -0.2}]}], {t, 0, 2 Pi, Pi/120}]
図3:立体の回転のステレオ立体視動画
図3はプログラム3で描かれた動画を示しています。図2と同様にして立体的に見ることができます。動画ファイルを作成する方法は前半で説明した通りです。
前回のスペースシャトルも同様にプログラム4で図4の動画のように回転させることができます。
<<プログラム4>>
Animate[GraphicsRow[{Show[ExampleData[{“Geometry3D”, “SpaceShuttle”}],
Boxed -> False, SphericalRegion -> True,
Background -> LightBlue,
ImageSize -> 300, ViewPoint -> 3. { Sin[t], Cos[t], -0.2}],
Show[ExampleData[{“Geometry3D”, “SpaceShuttle”}], Boxed -> False,
SphericalRegion -> True, Background -> LightBlue,
ImageSize -> 300,
ViewPoint -> 3. { Sin[t + Pi/20], Cos[t + Pi/20], -0.2}]}], {t, 0, 2 Pi, Pi/120}]
図4:スペースシャトルの回転のステレオ立体視動画
まとめ
今回はアニメーションを動画ファイルとして取り出す方法と裸眼立体視のアニメーションの作り方について説明しました。
ここまでは定義済みの立体を表示するだけでしたが、次回からは立体を動かしてアニメーションを作ってみたいと思います。ご期待ください。
参考文献:Mathematicaグラフィックスの入門書
中村健蔵「Mathematicaで絵を描こう」1997東京電機大学出版局
ノートブックのダウンロードについて
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。