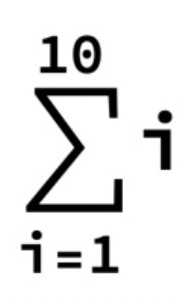要約:Mathematicaの式の入力・評価における注意事項と今後の理解に重要な関数、リストという概念について解説します。
Mathematicaのライブ計算
Mathematicaにはライブ計算というモードがあり、書いた数式を直接、評価することができます。例えば、次の様な場合です。
1+2+3
この計算をさせるには、シフト+リターンすれば良い。
重要
| なお、この段階で投げ出しそうになった友人がいるので、強調しておきますが、リターンではありません。シフト+リターン、もしくはエンターです。リターンでは文章が改行されるだけで、計算、つまり、式の評価はされないのでくれぐれも注意して下さい。 |
関数
関数を使って、上の式を書き換えたものが次です。
Plus[1,2,3]
関数はMathematicaの計算機言語の中では、非常に重要な概念です。各人で定義することもできますが、多くの組込関数があり、利用する方が初めは多いと思われます。一般的に 関数[引数,オプション] の形式で定義されており、引数には上の例の様な数字のデータ等を与える場合があります。また、組込関数は単語の最初の文字が大文字になっています。
リスト
もう1つ、重要な概念があります。数字などを1並びにしたものが、リストです。上の数字で考えると
{1,2,3}
で、ひとまとめにされた数字の並びです。この形式で合計を計算する関数は別にあります。
Total[{1,2,3}]
ここで気づいた人もいると思いますが、Mathematicaでは色々な括弧が使われています。関数の角括弧[]、リストの波括弧{}、計算式の括弧()などです。括弧は閉じていなければ文法上のエラーになるますが、Mathematica自体が閉じているかのチェックをしてくれるので、心配な場合は心配な括弧にカーソルを合わせてみれば確認できます。
さて、このリストを利用することがMathematicaの習得には非常に重要です。プログラミングで良く有る問題「1からnまでの整数の和」を計算することを考えてみましょう。
良く有るDo文を使って書いたものが次です。
n = 10; (*nの値*)
total = 0; (*総計の初期値*)
Do[total = total + i, {i, 1, n}]; (*Doループ*)
total (*総計を表示*)
55
ここで(**)は注釈で結果に影響を与えません。また、文末のセミコロン;は、文の区切りを示すとともに結果を表示しないようにしています。例えば、「文1; 文2; 文3」で一行となるとともに文3の評価結果が表示されます。もし、文3の評価結果も表示しなければ、「文1;文2; 文3;」とすれば良いわけです。
上のnの値を変えて再評価すれば、望みの数値が得られるわけです。
次にリストを使って同じ計算したものが、下です。
n = 10; (*nの値*)
Total[Table[i, {i, 1, n}]]
55
Tableはリストを作る関数で、Table[i, {i, 1, 10}]であれば、iを1から10まで変えながら、iのリストを作ります。つまり、{1,2,3,4,5,6,7,8,9,10}が出来るので、それをTotalして結果を得ているわけです。
ところでMathematicaには総和の関数も当然定義されており、教科書にある数式通りに入力すれば、計算してくれます。
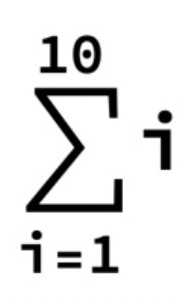
55
これを関数で書き直したものが、次です。
n = 10; (*nの値*)
Sum[i, {i, 1, n}]
55
さらに驚くべきことに、この関数は理論式を与えてくれます。
ClearAll[n];
Sum[i, {i, 1, n}]
n(n+1)/2
なお、ClearAll[n]; は、n = 10; と、前にnに数が代入されているので、属性等を消去しました。この結果、1からnまでの整数の和は理論式n(n+1)/2で与えられます。
したがって、この理論式を利用すれば、次で計算できます。これは究極のシンプル計算になります!
n = 10; (*nの値*)
n (1 + n)/2
55
このように無理やりループ計算しなくても計算できるものが多くあります。「数学は手を抜くための技術という一面もある」といった数学者がいましたが、名言です。例えば、1から10^23までの整数和を出すループ計算をしたら、どんなに計算が早いといっても、まずは計算資源の無駄です。力づくで計算する前に理論式について考えてみるべきでしょう。また、それが科学的思考と云うものでしょう。
また、Mathematicaでは組込関数が5千以上あると言われており、筆者も全てを使ったことは当然ありません。Mathematicaを使いこなしていくコツは、まずは使いたい組込関数を見つけることと考えています。オリジナルの問題には利用できる組込関数がないことも当然ありますが、ほとんどの場合は利用できるものが存在することが、これまでの私の経験です。まずは利用できる組込関数を探す、それが早道でしょう。これを強力に支援してくれるドキュメントやマニュアルがMathematicaの中にはあります。特にプルダウンメニューのヘルプの中にある「選択項目のヘルプ」は強力で、調べたい言葉や関数を選択したのちに「選択項目のヘルプ」を下図の通り指定すれば、例題を含めて解説してくれます。

図1:プルダウンメニューのヘルプの中にある「選択項目のヘルプ」
まとめ:Mathematica初学者のために式の評価の仕方、重要な概念である関数とリストについて説明しました。関数の細かい説明はしていませんが、実行しながら、「選択項目のヘルプ」で調べてみると良いでしょう。
参考文献:Mathematicaの入門書
1 Stephen Wolfram “An Elementary Introduction to the Wolfram Language” 2017 Wolfram Media
2 C・ヘイスティング「ハンズ・オン・スタートMathematica」2019丸善
3 中村健蔵「Mathematicaで絵を描こう」1997東京電機大学出版局
4 中村健蔵2019『MathematicaによるOR』楽天Kobo・キンドルDP