要旨:MBA取得のためのMathematica 2として、ゲーム理論の基礎的な内容である完全情報の2人ゼロ和ゲームと2人非ゼロ和ゲームについて述べ、その繰り返しについても言及する。なお、ノートブックのダウンロードについては末尾から出来ます。
さて、MBAとの関連であるが、ノーベル経済学賞でケネス・アローの一般均衡理論についての1972年度の受賞を皮切りに2016年までゲーム理論に関連するものが18回あり、経済理論を理解するためには欠かせないものであるだけでなく、個人・組織の対立・共存に対して考えておくべき深い示唆を与えてくれるものです。今回は基礎的な理論が主ですが、ジレンマゲームの繰り返しについても言及しており、次回につながるものと考えています。
1 全般
2人が競争している場合、一方の側の決定の効果が他方の側の決定によって低下させられる可能性を含んでいます。この点がゲーム理論の本質であり、これまでのものとは異なることです。例えば、線型計画法などは自分の計画を最適にすることだけを考えていたのですが、相手の決定により自分の効果が変わる場合、どうするべきかを考えようというものです。具体例としては将棋や麻雀などの室内遊技であり、また、実社会では経済・政治・スポーツさらには戦争などです。このような場合について解くための手法が所謂ゲームの理論なのです。
歴史的に、これらの競合の問題を理論的に考え始めたのは、電子計算機の発明者として有名なフォン・ノイマンです。彼は1928年、ゲームの基本定理を発表し、その後も研究を進め1944年には経済学者のモルゲンシュテルンとの共著「ゲームの理論と経済行動」として体形化されました。
ゲームを分類する場合、要因として参加者の人数・支払・情報の有無・選びうる手(戦術)の数などがあります。
(1)参加者の人数は利害が同じです。組織を1人と見做し数えたものです。従って、野球は2人ゲームです。なお、3人以上のゲームは2人ゲームと理論的な本質で異なります。
(2)支払はゲームの終了時に受け渡される価値であり、ある人が1だけ支払うとき受け取る側が1だけ受け取るという形で参加者全体のやり取りする金額の合計が0であれば、ゼロ和ゲームといいます。それ以外を非ゼロ和ゲームといいます。
(3)情報の有無:全ての参加者が他の参加者のそれ以前の手で選ばれた結果を完全に知って行動するとき完全情報ゲームといいます。
(4)選びうる手(戦術)の数が有限であるとき、有限ゲームといいます。
本章では、基本的な完全情報で有限な2人ゼロ和ゲーム及び2人非ゼロ和ゲームについて述べます。
2 2人ゼロ和ゲーム
ゲームの最も基本な形です。完全情報で有限な2人ゼロ和ゲームについて述べます。
2.1 ゲームの例
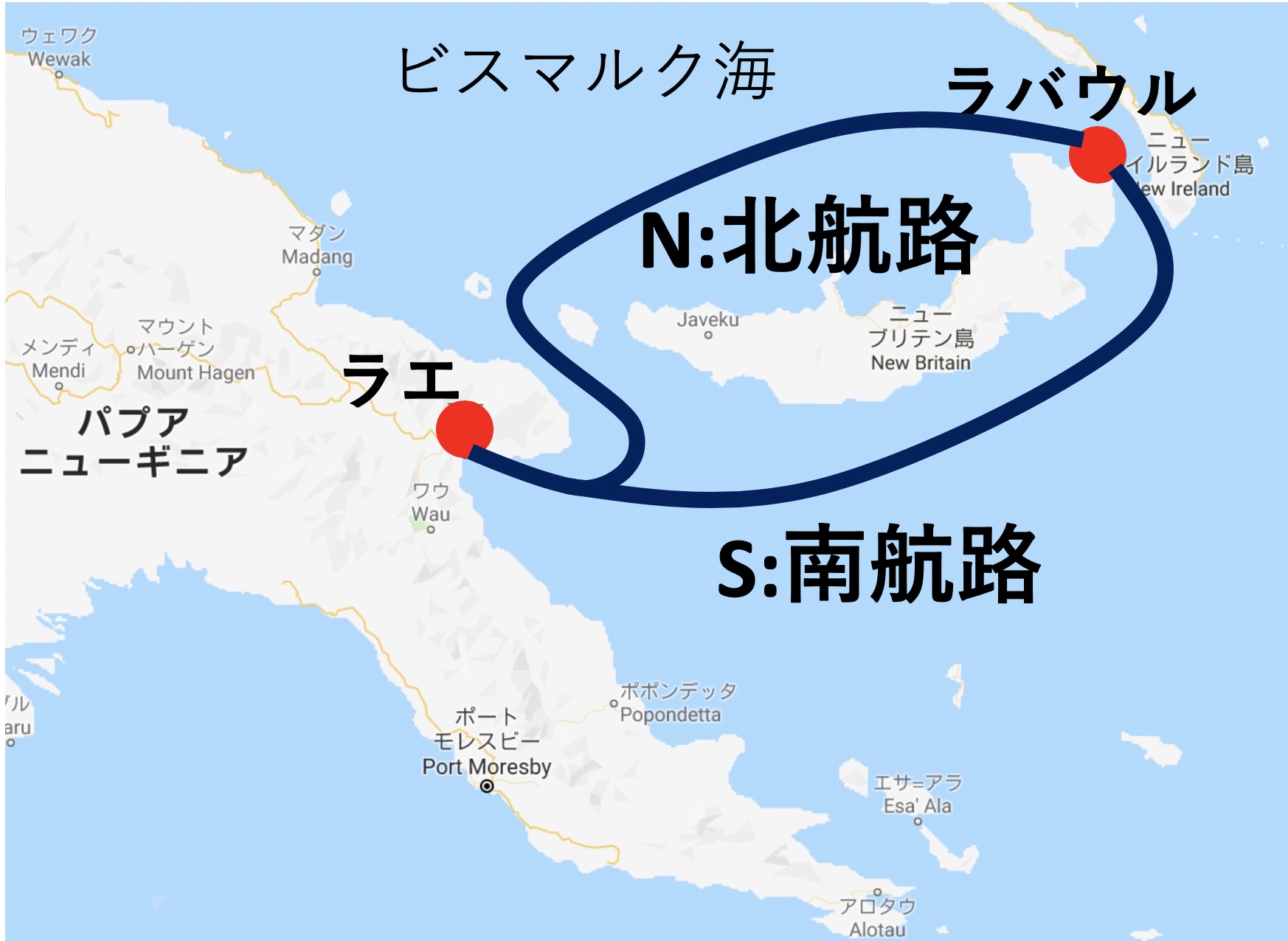
文献1にも簡単に記述されていますが、有名なゲームの例として太平洋戦争中の昭和18年3月に日米で戦われたビスマルク海海戦について考えてみましょう。図1はビスマルク海周辺です。ラバウルにいる日本軍はニューギニア島のラエにいる部隊に増援を行ないたい。増援するための南北の航路は共に3日間の行程を要します。一方、ポートモレスビーに司令部を置く米軍は増援を阻止するべく航空偵察と航空攻撃を準備していました。南航路はいつも快晴で視界がよく、簡単に見つけることができますが、北航路はスコールのため天候が悪く、偵察しても見つけにくく、また、航空攻撃できない可能性もありました。従って、偵察の重点を南北どちらの航路にするか迷っていました。
図1:ビスマルク海周辺(Google Mapを利用)
表1に日米が南北航路のどちらの選択をするかに応じる米軍の航空攻撃可能な日数を上げます。
表1:米軍の攻撃可能日数
| 日本軍 米軍 | 北航路 | 南航路 |
| 北航路 | 2 | 2 |
| 南航路 | 1 | 3 |
米軍が南航路に偵察の重点を置いた場合、日本軍が南航路で来れば、簡単に見つけることができるので3日間続けて攻撃をかけることができますが、北航路の場合には発見が遅れ、1日しか攻撃をかけられません。米軍が北航路に偵察の重点を置いた場合には、日本軍が南航路で来ても、また、北航路の場合にも発見できます。従って、日本軍がどちらから来ても2日は攻撃をかけることができます。
日米両軍の指揮官はどうするべきでしょうか。このような場合に最適なやり方を考えるものが、ゲームの理論です。
まず、結論から述べておくと、日米両軍とも北航路を選択し、戦闘の経過は、次のようなものでした。
2月28日 日本の艦隊がラバウルを出航(輸送船8隻、駆逐艦8隻)
3月1日 米軍の偵察機が北航路上の日本の艦隊を発見
3月2日 朝、爆撃機10機、夕、8機で攻撃し、輸送船1隻撃沈
3月3日 早朝より爆撃機のべ80機で反復爆撃。輸送船7隻と駆逐艦4隻を撃沈
ゲームの解法については後ほど述べますが、ゲームで使う言葉とゲームにはどんな種類があるかを考えてみましょう。
まず、ゲームを行なう人をPlayerと言う。上の場合には、米軍と日本軍です。各Playerが選択する対象を戦略(Strategy)又は方策(Policy)と呼びます。上では南北の航路のどちらを選ぶかということです。また、各戦略の組み合わせに応じて得られるものを支払い(Payoff)と呼んでいる。上の例では、米軍の攻撃可能日数を支払いと考えることができます。そして、米軍はこの支払いを最大に、日本軍は最小にしたいと考えているわけです。また、支払いの表を作る場合には、通常、最大化Playerを基準として作ります。
2.2 ゲームの解法
ビスマルク海海戦の例についてゲームを解くことを考えてみましょう。ここで相手の出方を決めてしまうと裏をかかれることになります。それを防ぐためには表2及び表3にあるように、先ず各戦略の支払いにおいて最悪の場合を考えて、その中で最も有利なものを取ればよいわけです。
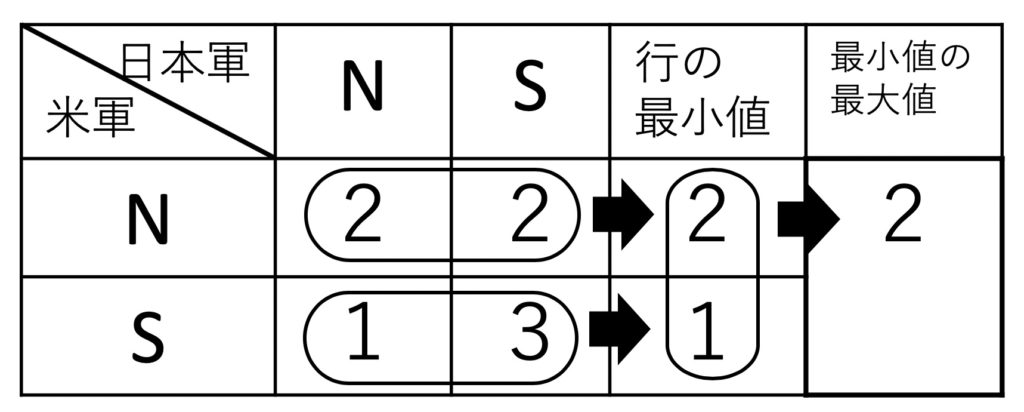
表2:米軍の戦略に応じるMinMax値
表2の米軍の場合は攻撃できる日数をできるだけ多くしたいのですから、先ず自分に不利な方(少ない攻撃日数)を選択します、つまり、南航路に偵察を準備した時には日本軍も北航路を取り、北航路の時はどちらの方を取っても同じです。従って、行の最小値2と1がそれぞれ選ばれることとなります。この2つの値の中で自分に有利(多い攻撃日数)な2(北航路)が選ばれることになります。
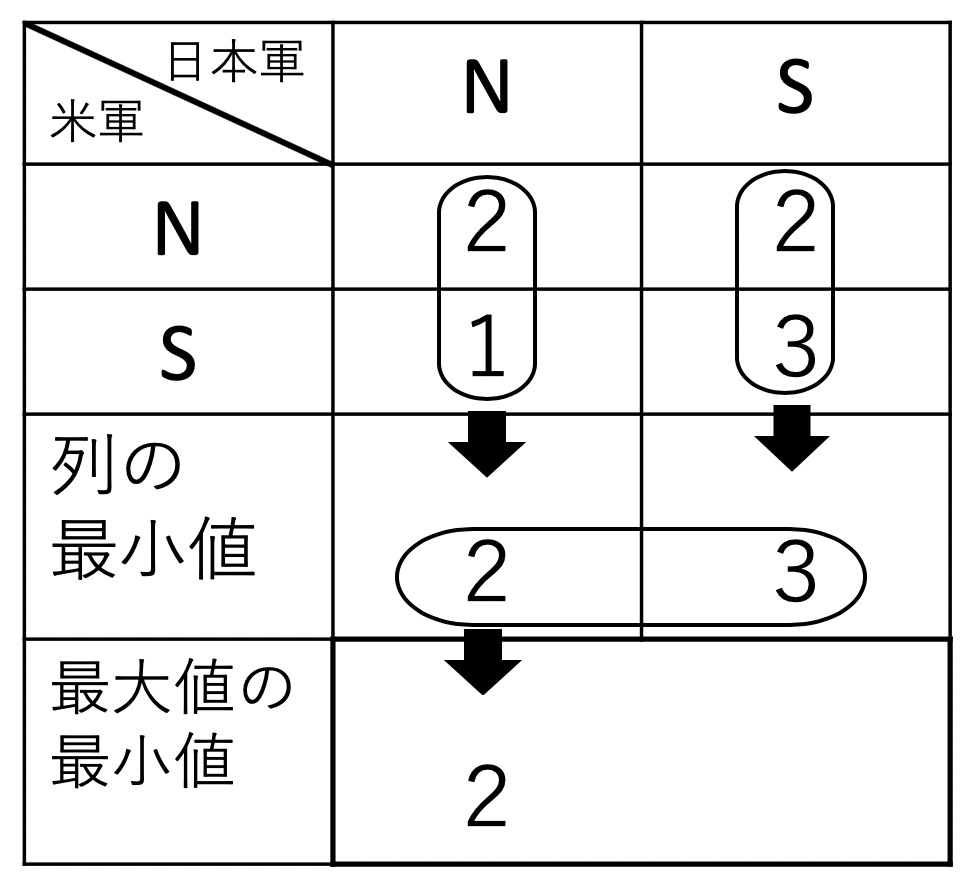
表3:日本軍の戦略に応じるMaxMin値
同様に表3の日本軍の場合は攻撃できる日数をできるだけ少なくしたいのですから、自分に不利な方、つまり、列の最大値2と3がそれぞれ選ばれることとなります。この中で自分に有利(少ない攻撃日数)な2(北航路)が選ばれることになります。
それぞれが、北航路を選択することになり、ゲームの値2を得る。このように考えられる最悪の場合のうちで最善に相当する戦略を選ぶことをMiniMax基準と呼んでいる。また、1つの戦略が選ばれる場合を純粋戦略と呼んでいる。
上の手順をMathematicaに行なわせたのが、リスト1にある関数puregameです。
<<リスト1>>
puregame[gamedata_]:=(*関数の定義*)
Module[{i,n,m,p={},q={},minrow,maxclm,maxminrow,minmaxclm},(*変数の定義*)
{n,m}=Dimensions[gamedata];(*行列の大きさ*)
minrow=Table[Min[gamedata[[i]]],{i,n}];(*行の最小値*)
maxminrow=Max[minrow];(*上の最大値*)
Do[If[maxminrow==minrow[[i]],p=i,],{i,n}];(*戦略*)
Print[“最大化Playerの戦略=“,p,(*表示*)
” ゲームの値= “,maxminrow];
maxclm=Table[Max[Transpose[gamedata][[i]]],{i,m}];(*列の最大値*)
minmaxclm=Min[maxclm];(*上の最小値*)
Do[If[minmaxclm==maxclm[[i]],q=i,],{i,m}];(*戦略*)
Print[“最小化Playerの戦略=“,q,(*表示*)
” ゲームの値= “,minmaxclm];
If[maxminrow==minmaxclm&&maxminrow==gamedata[[p,q]],(*純粋戦略の判定*)
Print[” “];Print[“鞍点を持ち、純粋戦略となる。“],
Print[” “];Print[“鞍点なし。混合戦略を調べてください。“]];
];
gamedata={{2,2},{1,3}};(*支払い行列*)
%//MatrixForm(*行列表示*)
2 2
1 3
puregame[gamedata](*関数の実行*)
最大化Playerの戦略=1 ゲームの値= 2
最小化Playerの戦略=1 ゲームの値= 2
鞍点を持ち、純粋戦略となります。
次に純粋戦略では解決できない場合について考えてみましょう。
2.3 混合戦略
ビスマルク海海戦では、南北航路とも3日の行程でしたが、ここで北航路は3日半かかると考えてみましょう。その時の米軍の攻撃可能日数は表4に示すように変化します。このゲームを関数puregameで解いた結果は、リスト2にあるように純粋戦略では解決できません。
表4:変形した米軍の攻撃可能日数
| 日本軍 米軍 | N | S |
| N | 2.5 | 2 |
| S | 1.5 | 3 |
<<リスト2>>
gamedata={{2.5,2},{1.5,3}};(*支払い行列*)
%//MatrixForm(*行列表示*)
2.5 2
1.5 3
puregame[gamedata](*関数の実行*)
最大化Playerの戦略=1 ゲームの値= 2
最小化Playerの戦略=1 ゲームの値= 2.5
鞍点なし。混合戦略を調べてください。
このようにPlayerの戦略が一致せず、純粋戦略では解決できない場合には、北航路をpの確率で選び、南航路を1ーpの確率で選ぶような戦略を考える必要があります。このような戦略を混合戦略と呼びます。日米両軍がそれぞれ北航路をx、yの確率で選ぶ混合戦略を考えたときの支払いの期待値は次の式で示されます。
E(x,y)=2.5xy+2x(1-y)+1.5(1-x)y+3(1-x)(1-y)
=3 – x – 1.5 y + 2 x y
最大化Player(米軍)は、最小化Player(日本軍)がそれぞれの戦略で来たときの期待利得E(x,0)とE(x,1)を図2に示す。図2においてx=0.4を表示していますが、x=0.4においてどんなに努力してもE(x,1)の制約から極大値以上の利得は期待できなません。従って、線形計画法と同様に最大化する場合に条件を満たさない部分をハッチングすると、条件を満たす部分がハッチングされずに残ります。その中で図2で最大値として示した部分が期待利得最大の点であることは明らかです。その点を線形計画法で使用した関数ConstrainedMaxを用いて求めたものがリスト4です。その結果から米軍は、北航路を0.75、南航路を1-0.75=0.25の確率で選択して偵察させればよいわけです。
<<リスト3>>
gain[x_,y_]:=Expand[2.5x y+2x(1-y)+1.5(1-x)y+3(1-x)(1-y)];(*期待利得*)
gain[x,y]
3 – x – 1.5 y + 2. x y
Plot[{4,gain[x,0],gain[x,1]},{x,0,1}, Fill->{1}] (*作図*)
<<リスト4>>
ConstrainedMax[expectgain,(*最大値を求める*)
{expectgain-gain[x,0]<0,
expectgain-gain[x,1]<0},{x,expectgain}]
{2.25, {x -> 0.75, expectgain -> 2.25}}
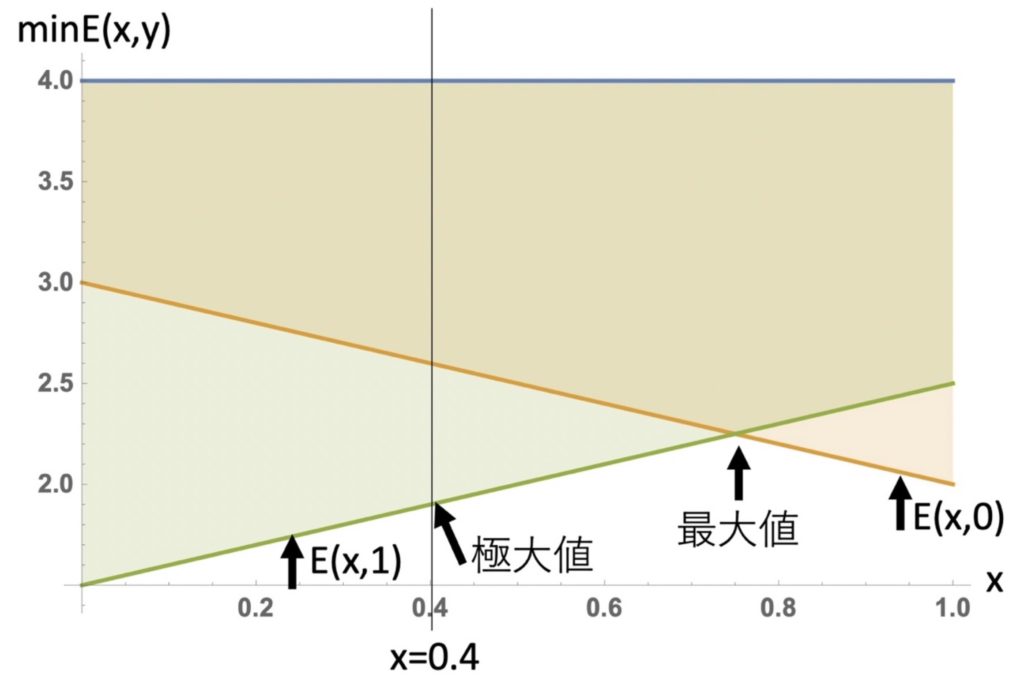
図2:最大化playerの許容領域
米軍と同様に日本軍についてもyの確率で北航路を選ぶとして混合戦略をリスト5及びリスト6により解いてみます。リスト5で書いた図3から最小値は明白です。リスト6の結果から日本軍は、北航路を0.5、南航路を0.5の確率で選択して増援すればよい。ここで注意しなければいけないのは、日米両軍の期待利得は共に2.25で、同じになっている点です。
<<リスト5>>
Plot[{0,gain[0,y],gain[1,y]},{y,0,1},(*作図*) Filling -> {1}]
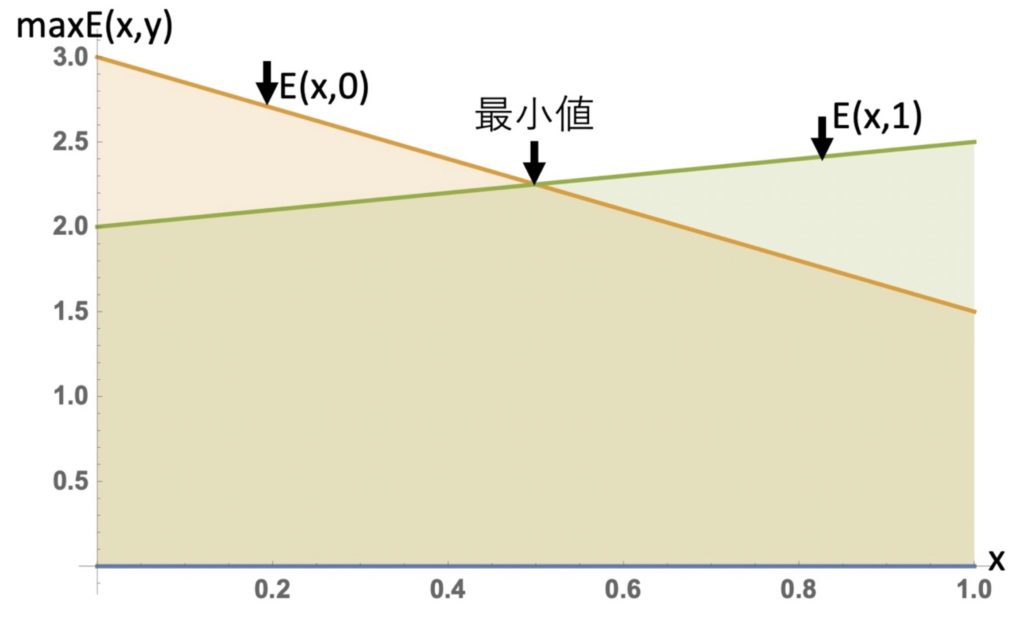
図3:最小化playerの許容領域
<<リスト6>>
ConstrainedMin[expectgain,(*最小値を求める*)
{expectgain-gain[0,y]>0,
expectgain-gain[1,y]>0},{expectgain,y}]
{2.25, {expectgain -> 2.25, y -> 0.5}}
戦略が3つ以上ある場合には、上の様に図を使い解くことは出来ません。次に戦略が3つ以上ある場合の解法について述べます。
2.4 ジャンケン
それぞれの戦略が3つあるゲームの例としてジャンケンを考えてみましょう。誰でも知っているようにジャンケンは、例えばグーだけを出せば勝つということはありませんが、ジャンケンにも必勝法は存在するのでしょうか。
AさんとBさんがジャンケンをしました。ご存じの通りですが、例えば、Aさんがグーを出して、Bさんが同じくグーを出せば引き分けであり、BさんがチョキであればAさんの勝ちです。ここで支払いは、勝ちで1、負けでー1、また、引き分けで0を与えられるものとします。勝敗に応じる支払いを表5に示しました。
表5:Aさんの支払い
| Bさん Aさん | グー | チョキ | パー |
| グー | 0 | 1 | -1 |
| チョキ | -1 | 0 | 1 |
| パー | 1 | -1 | 0 |
結論から言うと有限なゼロ和2人ゲームは、線形計画法を使って解くことができます。以下、線形計画法として定式化してみましょう。なお、文献3には、ゲームを線形計画法で解く方法が記されているので参考にしました。
先ず、ゲームの値が正です。ようにするために表5の支払い行列に1を加えて新しい表6を得ました。
表6:補正した支払い
| Bさん Aさん | グー | チョキ | パー |
| グー | 1 | 2 | 0 |
| チョキ | 0 | 1 | 2 |
| パー | 2 | 0 | 1 |
ここでAさんはグー・チョキ・パーをそれぞれx1,x2,x3の確率で選択するものとします。vが期待利得を表すとすると。
x1+2 x3≧v
2 x1+x2≧v
2 x2+x3≧v
かつx1+x2+x3=1の条件でvを最大にするようなx1,x2,x3を求めることです。
v>0に注意して と置くと上の問題は
X1+2 X3≧1
2 X1+X2≧1
2 X2+X3≧1
X1,X2,X3≧0
の条件の元で
X1+X2+X3=1/v
を最小にするX1,X2,X3を求める問題に帰着します。
上を関数ConstrainedMinでリスト7により解きます。なお、期待利得は支払い行列を変形しているので、1-1=0に還元する必要があります。
<<リスト7>>
gamedata={{0,1,-1},{-1,0,1},{1,-1,0}}-(-1);(*支払い行列の変形*)
%//MatrixForm(*マトリックス表示*)
1 2 0
0 1 2
2 0 1
ConstrainedMin[x1+x2+x3,(*線形計画法として解く*)
{x1+2 x3>1,2 x1+x2>1,2 x2+x3>1},{x1,x2,x3}]
{1, {x1 -> 1/3, x2 -> 1/3, x3 -> 1/3}}
上で説明した手順によりゲームを線形計画の問題に定式化し、解くことができるので、最大化・最小化Playerの両方について混合戦略を解くための関数mixedstrategyをリスト8で定義し、ジャンケンの例を解いてみました。なお、この関数では当初、ゲームの値を正にするための補正を行なっていますが、最後に期待利得を元の問題に補正し直しています。
<<リスト8>>
mixedstrategy[gamedata_]:=(*関数の定義*)
Module[{minielement,game1,n,m,gamevalue,strategy},(*変数の定義*)
minielement=Min[gamedata];(*行列の最小値*)
If[minielement<0,(*行列の補正*)
game1=gamedata-minielement,game1=gamedata];
{n,m}=Dimensions[game1];(*行列の大きさ*)
strategy=LinearProgramming[Table[1,{i,n}],(*線形計画法として解く*)
Transpose[game1],Table[1,{i,m}]];
gamevalue=1/(strategy.Table[1,{i,n}]);(*期待利得*)
strategy=gamevalue strategy;(*戦略の還元*)
If[minielement<0,gamevalue+=minielement,];(*期待利得の補正*)
Print[“最大化Playerの混合戦略= “,strategy];(*表示*)
Print[“ゲームの値= “,gamevalue];
Print[” “];Print[” “];
strategy=LinearProgramming[Table[-1,{i,m}],(*線形計画法として解く*)
-game1,Table[-1,{i,n}]];
gamevalue=1/(strategy.Table[1,{i,m}]);(*期待利得*)
strategy=gamevalue strategy;(*戦略の還元*)
If[minielement<0,gamevalue+=minielement,];(*期待利得の補正*)
Print[“最小化Playerの混合戦略= “,strategy];(*表示*)
Print[“ゲームの値= “,gamevalue];
];
gamedata={{0,1,-1},{-1,0,1},{1,-1,0}};(*支払い行列*)
%//MatrixForm
0 1 -1
-1 0 1
1 -1 0
mixedstrategy[gamedata](*解法の実行*)
最大化Playerの混合戦略= {1/3, 1/3, 1/3}
ゲームの値= 0
最小化Playerの混合戦略= { 1/3, 1/3, 1/3}
ゲームの値= 0
解けることは分かって頂けたと思いますので、ここでジャンケンの注意事項について考えてみましょう。
リスト8の結果では、ジャンケンをする場合には、グー・チョキ・パーをそれぞれ均等な1/3の確率で選ぶべきことが示されています。当然のことのように思えますが、自分がジャンケンをしている時のことを考えると、本当に均等な確率で出しているでしょうか。
例えば、グーを出して負けたので次はチョキにしてみようなどと考えたり、相手はグーを良く出すのでパーにしてみようなどと読んだりしているのではないでしょうか。つまり、グー・チョキ・パーの出し方には偏りや連の出方、グーの後はパーなどといった傾向が通常あるものなのです。従って、ゲームの理論からの注意事項は均等に出すべしということになります。これが非常に難しいので、独自の方法を考えてみて下さい
さて、総括すると有限なゼロ和2人ゲームについては、先ず、関数puregameで純粋戦略があるかどうかを調べ、無かった場合には関数mixedstrategyで混合戦略を解けばよい。戦略の数は2個以上有限であればよいということです。
リスト9は、関数mixedstrategyを使い変形したビスマルク海海戦の例を解いたものです。当然ですが、先の解と同じ結論になっています。
<<リスト9>>
gamedata={{2.5,2},{1.5,3}};(*変形したビスマルク海戦の支払い行列*)
%//MatrixForm
2.5 2
1.5 3
mixedstrategy[gamedata](*解法の実行*)
最大化Playerの混合戦略= {0.75, 0.25}
ゲームの値= 2.25
最小化Playerの混合戦略= {0.5, 0.5}
ゲームの値= 2.25
3 2人非ゼロ和ゲーム
もっとも基本的でしかも数学的に完全に研究された2人ゼロ和ゲームについて述べましたが、2人非ゼロ和ゲームについては、現在研究が進められている現状であり、研究し尽くされたとは言い難いようです。理論的にも難解になり、本書の範囲を超えますので、代表的なものの概要について説明し、その戦略に応じる対戦シミュレーションについて考察します。
3.1 2人非ゼロ和ゲームの利得行列
非ゼロ和のゲームはゼロ和のものと異なり、一方が2を得たときに相手はー2を得るというものではない。したがって、その利得行列は双方の得たものを記入する形で表のように表わされます。
表7:2人ゲームの利得行列の比較
| Aの戦略 Bの戦略 | 戦略a | 戦略b |
| 戦略ア | 3 | 4 |
| 戦略イ | 4 | 2 |
2人ゼロ和ゲームの利得
| Aの戦略 Bの戦略 | 戦略a | 戦略b |
| 戦略ア | 3,3 | 1,4 |
| 戦略イ | 4,1 | 2,2 |
2人非ゼロ和ゲームの利得
3.2 代表的な2人非ゼロ和ゲームの例
有名な2人非ゼロ和ゲームとして囚人のジレンマというものがあります。それは、次のようなものです。「ある事件で犯人が2人捕まった。2人は別々の部屋で取り調べを受けています。それぞれの対応としては、黙秘をするか、自白をするかの2つの方法があります。もし、2人共に黙秘をすれば、犯罪が立証できないため2年程度の刑が予想されます。逆に2人ともに自白をすれば、犯罪は解明されますが、自白を考慮して2人共に4年の刑となります。また、1人が自白し、1人が黙秘すれば、一方の自白で犯罪は立証され、黙秘したほうは5年の刑、自白したほうは情状酌量により無罪放免となります。」これを利得行列として表わすと、次のようになります。なお、与えられる刑の年数ですので利得という点からは、マエナスを付けたほうが感覚に合うでしょう。
表8:囚人のジレンマの利得行列
| Aの対応 Bの対応 | 自白 | 黙秘 |
| 自白 | -4,-4 | 0,-5 |
| 黙秘 | -5,0 | -2,-2 |
利得行列を一見すると、2人ともに黙秘をしたほうが共に2年の刑で済むのでよいように感じられるが、自分が黙秘をしたときにもう一方に裏切られ自白されると最高刑の5年を受けることになる恐怖から結局2人ともに自白することに落ち着いてしまうのです。 「お互いに協調すれば、最良であるのは分かっていながら、自分の利益を追及すると最悪に陥ってしまう。」このようなジレンマの例はいろいろなところで見ることができます。例えば、価格競争などでしょう。
3.3 ナッシュ解
ナッシュ解とは、自分だけが選択を変えると損になってしまうような解を言います。上の囚人のジレンマの例では、両方が黙秘をする場合は自分だけが選択を変えると利益になってしまうので、ナッシュ解にはなっていません。両方が自白の場合には、自分だけが選択を変えて黙秘してしまうと損になってしまうので、ナッシュ解になっていることが分かります。
従って、両方とも黙秘をした場合がいいことは分かっていながら両方ともに自白してしまうということに落ち着いてしまうのです。
ナッシュ解を解くパッケージが文献2で紹介されています。囚人のジレンマなど興味深い話題も多いので、非ゼロ和2人ゲームを解く必要のある人はそちらを入手されることをお薦めします。
3.4 囚人のジレンマの繰り返し
囚人のジレンマは、1回だけの話でしたが、これを何回も繰り返したらどうでしょうか。学習の効果から裏切りだけでなく協調も出てくることが予想されます。
ところで、囚人のジレンマでは、特殊な事例で繰り返し行っても余り意味が無いように感じられるかもしれませんが、同じ利得行列を持つ共同作業の場合で考えたら、よくある人生の一コマを見るような感じられるのではないでしょうか。
表9:共同作業の利得行列
| Aの対応 Bの対応 | 協力 | 裏切り |
| 協力 | 3,3 | 0,5 |
| 裏切り | 5,0 | 1,1 |
2人の人が自分の家の近くの共同場所で清掃作業をやることにしました。二人が協力してやれば、それぞれ3ずつの利得が得られます。しかし、一人が裏切り1人だけで清掃をやったとき、裏切ったほうは自分ではやらずに清掃が終わったのだから5の利得を得ますが、清掃をやったほうは気分が害して0の利得しか得られません。しかし、二人がともにやらなかったら清掃場所はきれいにはなりませんが、自分がやった訳でもないので諦めがつき、それぞれ1ずつの利得です。
また、囚人のジレンマと同じ利得行列を持つといいましたが、これはそれぞれの利得から5を引いて、自白と黙秘の順番を逆にして見ると同じ利得行列であることがわかります。
さて、共同作業を行うことを繰り返すわけですが、どのようなルールで戦略を選ぶことがよいのでしょうか。ところで戦略を選択するルールのことをメタ戦略と呼びますが、次の3つのメタ戦略を考えみましょう。
(1)デタラメ戦略:等しい確率で裏切りか協調を選ぶ。
(2)裏切り戦略:常に裏切る
(3)しっぺ返し戦略:協調を基本とするが、相手が裏切ったら、次の回に裏切ってしっぺ返しをします。
リストでは、それぞれを相互に100回対戦させ、各メタ戦略から出た戦略を比較し、その利得を加えていって、総利得を比べてみようとするものです。alist、listbはそれぞれの出した戦略のリストですが、この3つのメタ戦略では使用していません。もっと複雑なメタ戦略を考えるときには使用するかもしれないので、一応残してあります。
なお、リストにおいてaの戦略はしっぺ返し戦略であり、bの戦略はデタラメ戦略です。また、裏切り戦略の時の関数は、strategy[]:=2で示されます。
<<リスト10>>
dilemmagame[]:=(*関数の定義*)
Module[{k=100,a=b=amark=markb=i=lasta=blast=0,
alist=listb={},a1b1=a1b2=a2b1=a2b2=0},
Print[“繰り返しの数=”,k];
astrategy[]:=If[a==0,1,blast];(*前者の戦略:しっぺ返し戦略*)
strategyb[]:=Random[Integer,{1,2}];(*後者の戦略:デタラメ戦略*)
(*裏切り戦略:strategy[]:=2*)
While[i<k,i++;
a=astrategy[];b=strategyb[];
If[a==1,If[b==1,amark+=3;markb+=3;a1b1+=1,
amark+=0;markb+=5;a1b2+=1],
If[b==1,amark+=5;markb+=0;a2b1+=1,
amark+=1;markb+=1;a2b2+=1]];
AppendTo[alist,a];AppendTo[listb,b];
lasta=a;blast=b
]
Print[“前者の点数=”,amark,”後者の点数=”,markb];
Print[“a1b1=”,a1b1,” a1b2=”,a1b2];
Print[“a2b1=”,a2b1,” a2b2=”,a2b2];
];
dilemmagame[]
k=100
amark=227 markb=232
a1b1=22 a1b2=29
a2b1=28 a2b2=21
各メタ戦略に応じる総得点を表10に示しました。このとき、*で示したものは、乱数を使っていないので確定した値です。その他のものについては、乱数の出る目に応じて変化する概略の値です。しかしながら、100回の繰り返しを行っているのです。ある程度平均化されているものと考えて良いでしょう。また、両方ともデタラメ戦略のときは、それぞれの得点が異なるので、両者の平均点を持ってデタラメ戦略の得点としました。従って、0.5の端数が出ています。
表10:各メタ戦略に応じる総得点(*は、乱数を使っておらず確定した値)
| デタラメ戦略 | 裏切り戦略 | しっぺ返し戦略 | 総得点 | |
| デタラメ戦略 | 222.5 | 45 | 232 | 499.5 |
| 裏切り戦略 | 320 | 100* | 104* | 524 |
| しっぺ返し戦略 | 227 | 99* | 300* | 626 |
総得点を見るとしっぺ返し戦略が最高得点であることが分かります。しかし、しっぺ返し戦略は、デタラメ戦略及び裏切り戦略のどちらにも負けているのです。
この不思議なしっぺ返し戦略の性質について考えてみると、このメタ戦略は、自分からは決して裏切らないことです。しかし、相手が裏切ったらすぐに報復をします。その一方で相手が協調を示したときにも即座に反応します。さらに裏切られても1回報復をするだけで、その禍恨をその後に残さないという単純明快なメタ戦略です。
<<その他のジレンマゲーム>>
上で示した囚人のジレンマは有名ですが、これだけがジレンマゲームではありません。良く似たものに弱虫ゲームがあるので紹介します。ところで、ジェームスディーンの映画「理由なき反抗」の中にチキンゲームというものが出てくるのをご存じでしょうか。この映画の中のチキンゲームは、2台の車で崖に突っ込んで早く車を飛び降りたものが負けというものでした。このようにアメリカで蛮勇を競うためにやるのがチキンゲームですが、もちろんチキンは雌鶏で、日本語に意訳すると「女の腐った奴」=弱虫となります。つまり、チキンゲーム=弱虫ゲームとなるわけです。

図4:チキンゲーム
映画の場合とは異なるが、一般的に弱虫ゲームは、次のようなものを考えていただけばよい。対向した2台の車をまっすぐな道路の上に離して置き、それぞれを運転し、衝突の恐怖に打ち勝って相手が避けるまでハンドルを切らずに我慢できるかで、その蛮勇を競うというものです。この弱虫ゲームの利得行列を考えてみましょう。この結果として図に示した3つが考えられます。1つは2人ともに強気で突っ込んで言って衝突した場合には、両方が少なくとも怪我を負い、車を壊してしまう最悪の結果となります。片方が、弱気でハンドルを切った場合には、衝突は回避されて最悪の結果になるのは避けられますが、ハンドルを切った方が弱虫のレッテルを張られることになります。両方が弱気で避けた場合には、回りで見ている者にとっては喜劇ですが、衝突もせず、名誉も傷つけられずにまあまあの結果です。これを利得行列にしたものが、表11です。
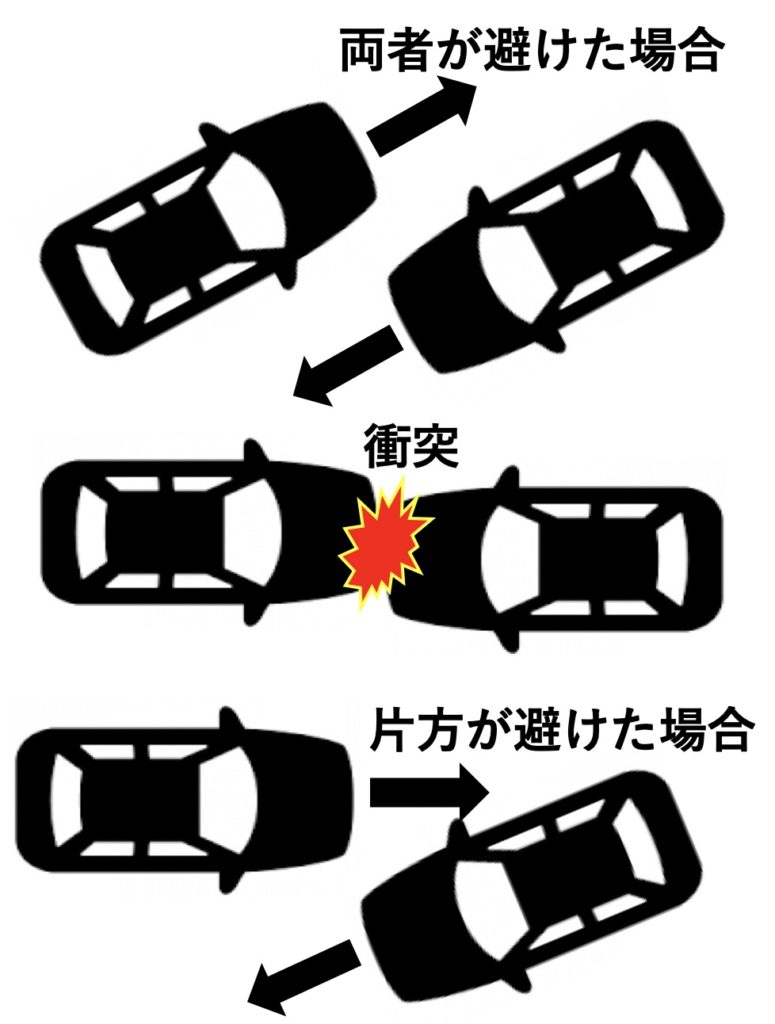
図5:チキンゲームの結果
表11:弱虫ゲームの利得行列
| Aの対応 Bの対応 | 弱気 | 強気 |
| 弱気 | 3,3 | 1,5 |
| 強気 | 5,1 | 0,0 |
この弱虫ゲームも世の中でよく見る有様で、夫婦喧嘩を考えれば身に詰まされるものがあります。これについても繰り返しをしてみると、「強気か、弱気か、それが問題だ」というように取るべき戦略を明らかにして見ると面白いでしょう。
考える手始めとして弱虫ゲームについても、次の3つのメタ戦略を考えみましょう。
(1)デタラメ戦略:確率pで弱気を選ぶ。
(2)強気戦略:常に強気で行動する。
(3)弱気戦略:常に弱気で行動する。
実は、この3つのメタ戦略であれば、囚人のジレンマのようにシミュレーションをする必要がなく、デタラメ戦略の確率pに応じて得られる得点の平均は簡単に算定できます。それぞれの得点は次の通りです。
(1)デタラメ戦略:500+500*p -300*p^2
(2)強気戦略:500+500*p
(3)弱気戦略:500+200*p
この式を確率pを0から1まで変化させたものが、図6です。図6では水平軸をデタラメ戦略の確率p、垂直軸を得点で示し、青で強気戦略、赤で弱気戦略、黄色でデタラメ戦略を示しています。
デタラメ戦略は5/6で最大値を取ります。しかしながら、常に強気戦略>デタラメ戦略>弱気戦略の順で並んでいます。3つの戦略が同じ値を取るのは、p=0、つまり、デタラメ戦略が強気戦略を取るときだけです。また、この時の全体の利得の合計は最低となります。世の中に強気ばかりが横行すると世の中全体の効率は悪くなると解釈できるでしょう。チキンゲームについては、囚人のジレンマのように研究されていないようであり、しっぺ返し戦略のような戦略は知られていません。しかし、先程述べたように世の中を見渡すとよく目にする光景であることから、チキンゲームについても最適戦略を考えてみるのも、自分の人生を考える上での大きな示唆があるかもしれません。
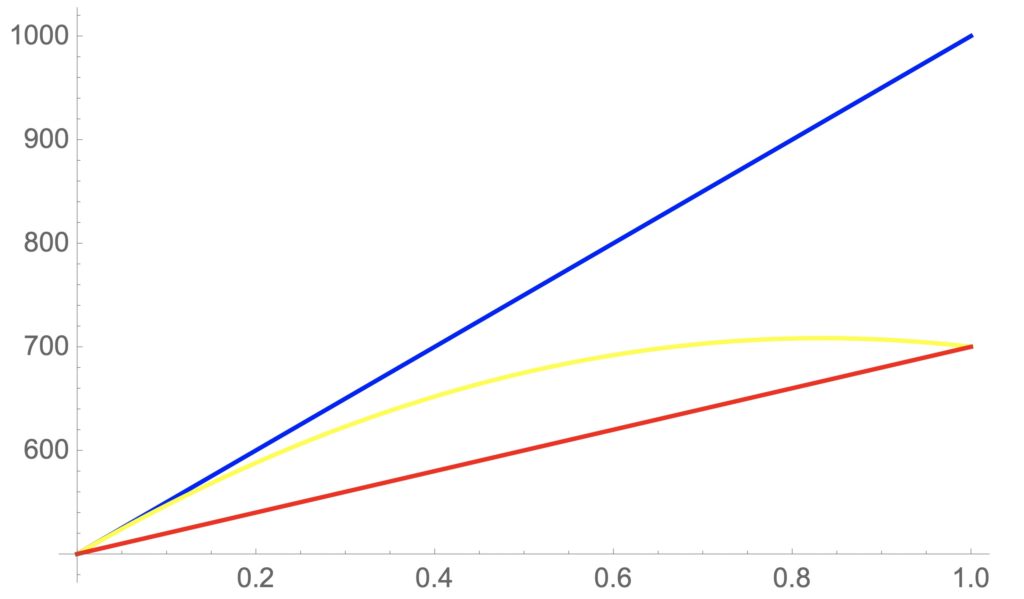
図6:チキンゲームの利得
<<参考文献>>
1 M.D.デービス著、桐谷・森訳、ブルーバックスBー217「ゲームの理論入門」1973、講談社
2 J.Dichant & T.Kaplan著、”A Program for Finding Nash Equilibria” pp87 Mathematica Journal, Vol.1-4 Spring 1991,Addison-Wesley Publishing Company
3 金田数正著、「OR手法とFORTRAN」1983、(株)内田老鶴圃
4 エリック・ラスムセン著、細江・村田・有定訳、「ゲームと情報の経済分析」1990、九州大学出版会
5 中村健蔵2019『MathematicaによるOR』楽天Kobo・キンドルDP
ノートブックのダウンロードについて
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。