要旨:MBA取得のためのにコンビニ全盛時代にも知っておかなければならない在庫管理の基礎について知り、Mathematicaによる算定と簡単なシミュレーションを行う。
なお、ノートブックのダウンロードについては末尾から出来ます。
1 全 般
コンビニ全盛において在庫管理は、あまり重要視されていない風潮が見られるようです。POS:Point of Salesシステムのような最先端の売り場では、売れたものを次の補給で充填して行くある意味単純なものになりました。しかし、バックヤードにおいては、複数の店舗に欠品なく、在庫をできるだけ少なくして管理していかなければなりません。さらに天気予報と連動した販売予測などと連携が行われており、現在、そして、今後も在庫管理が、企業において重要な役割を果たしていることは疑う余地がないと思われます。特に重要な機能は、有機的に連結された生産・販売のシステムにおける変動を吸収し、それぞれに独立性を持たせることです。
ここの内容は基本的な在庫管理について述べたものですが、POSシステムを想像しながら、基本的考え方をしっかりと抑えてください。
在庫管理において、いつ・どのくらい発注するかという発注時期と発注数量が特に問題であり、代表的な管理方式としては、在庫量が一定の在庫水準まで下がったら、一定量だけ注文していく発注点法と発注時期を一定にし、その際の発注量をかえて行く定期発注法の2つがあります。
まず、簡単な発注点法の場合のシミュレーションを行ないます。「店屋の場合、当初ある量(io)の商品の在庫をもっています。徐々に売れていき、ある量(o1)になったとき問屋に発注します。発注してからある日数(l1)が経ってから注文した量(i1)が到着しそれを元にまた商売を続けていく。」
なお、本シミュレーションにおいては売れ方は平均e1及び標準偏差s1の正規分布に従うものとしています。
ここで、問題となるのは、在庫の量と売り切れにならないために、いつ発注すべきかということです。次節では、それらについてさらに詳しく見て行きましょう。
<<リスト1>>
nmlrnd[e_,std_]:=
N[e+std*Cos[2 Pi Random[]]*Sqrt[-2 Log[Random[]]]];(**)
inventory[e1_,s1_,i0_,i1_,o1_,l1_,l2_]:=
Block[ {l=0,i=i0,a={i0},of=0,l3},
While[l<l2,l++;
i=i-Round[Abs[nmlrnd[e1,s1]]];
If[i<=o1 && of==0,of=1;l3=l+l1,];
If[of==1 && l3<=l,i=i+i1;of=0, ];
a=Append[a,i];
];
ListPlot[a,PlotJoined->True];
]
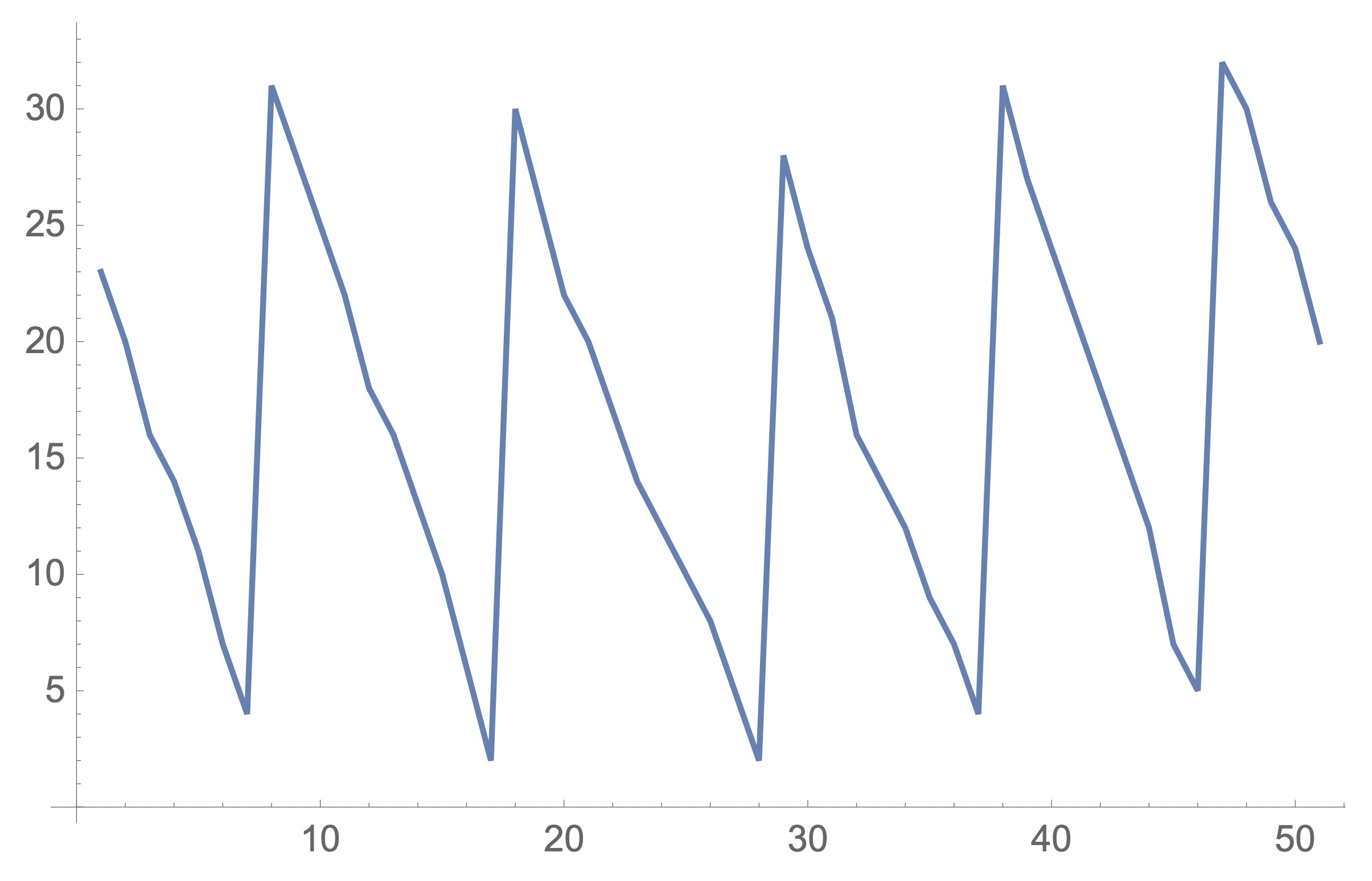
「ある店屋が、当初23の在庫を持っています。徐々に売れていき、在庫が7になったとき問屋に発注します。発注してから2日が経ってから注文した30が到着し、それを元にまた商売を続けていきます。また、平均3及び標準偏差1の正規分布に従う売れ方をしているものとしています。」の場合、inventory[3,1,23,30,7,2,50]で図1のようなシミュレーションを実施することができます。
図1の場合には、在庫切れも起こらず商売が行なわれています。次の発注点法では、いつ・いくつ発注するかが問題となります。
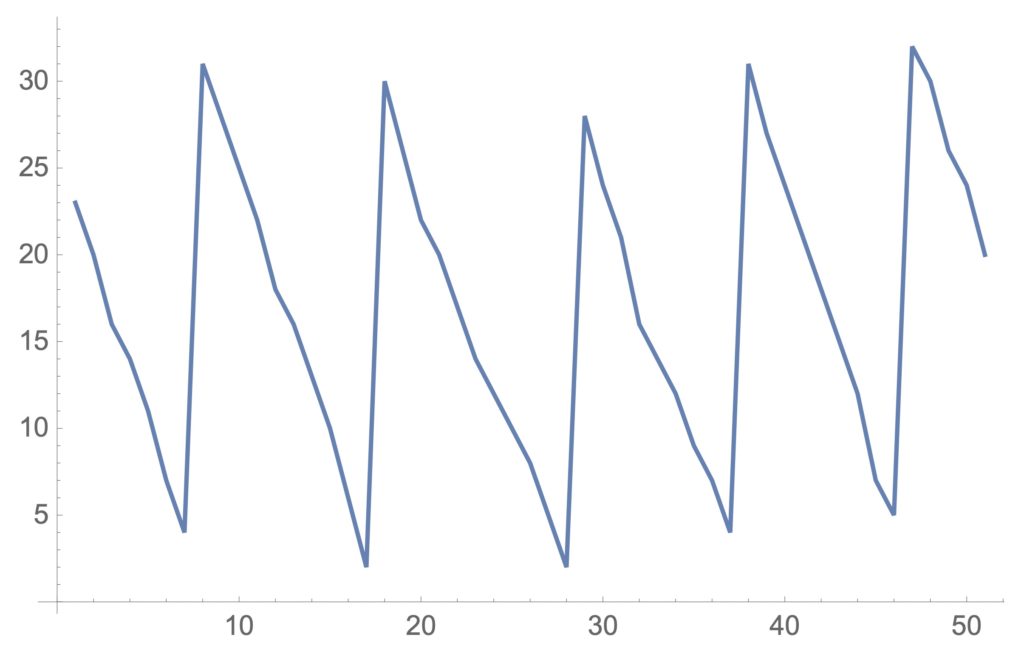
図1:発注点法の一例
2 発注点法(定量発注法)
前節のシミュレーションは、この方式をシミュレートしたものですが、これは在庫量が一定の在庫水準まで下がったら、一定量だけ注文していく方法です。
2.1 最適注文量
発注点法による最適注文量Qは次の公式が求められています。
ここで、r:年間総売上量
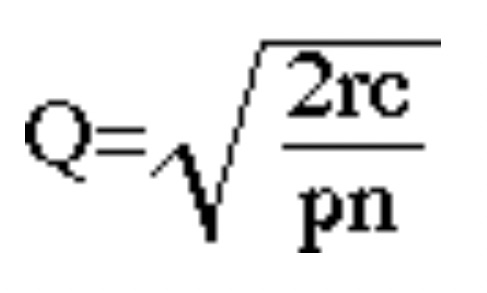
c:1回の注文費用
p:製品の単価
n:年間在庫保管率
従って、pnは製品1単位の年間在庫費用を表すことになります。
このとき、最適発注量Qは、q[r_,c_,p_,n_]:=N[Sqrt[2*r*c/(p*n)]]で求めることができます。
ある商品は年間を通じてほぼ一定の売上率であり、総売上量は2400です。商品の単価は500円、商品1個を1年間在庫したときの保管費の単価に対する百分率、即ち、年間在庫保管率は10%、1回の注文費用は1000円です。このときの最適発注量を求めてみます。
q[2400,1000,500,0.1]
309.84
この意味を考えてみましょう。年間に掛かる在庫の経費を最小限にすることが最適の条件です。
在庫の経費=年間在庫保管費用+年間注文費用です。
ここでkを年間の注文回数とすると経費は、yc[r_,c_,p_,n_,k_]:=r/k/2.*p*n + c*kで算定できます。リストにより、年間の注文回数を1〜12まで変化させてプロットしたものを図2に示しました。
<<リスト2>>
a=Table[{i,yc[2400,1000,500,.10,i]},{i,1,12}];(*経費の計算*)
Print[a];(*結果のプリント*)
ListPlot[a,PlotJoined->True ,
PlotRange -> {{0, 12}, {15000, 35000}}](*グラフ表示*)
{{1, 61000.}, {2, 32000.}, {3, 23000.}, {4, 19000.},
{5, 17000.}, {6, 16000.}, {7, 15571.4}, {8, 15500.},
{9, 15666.7}, {10, 16000.}, {11, 16454.5}, {12, 17000.}}
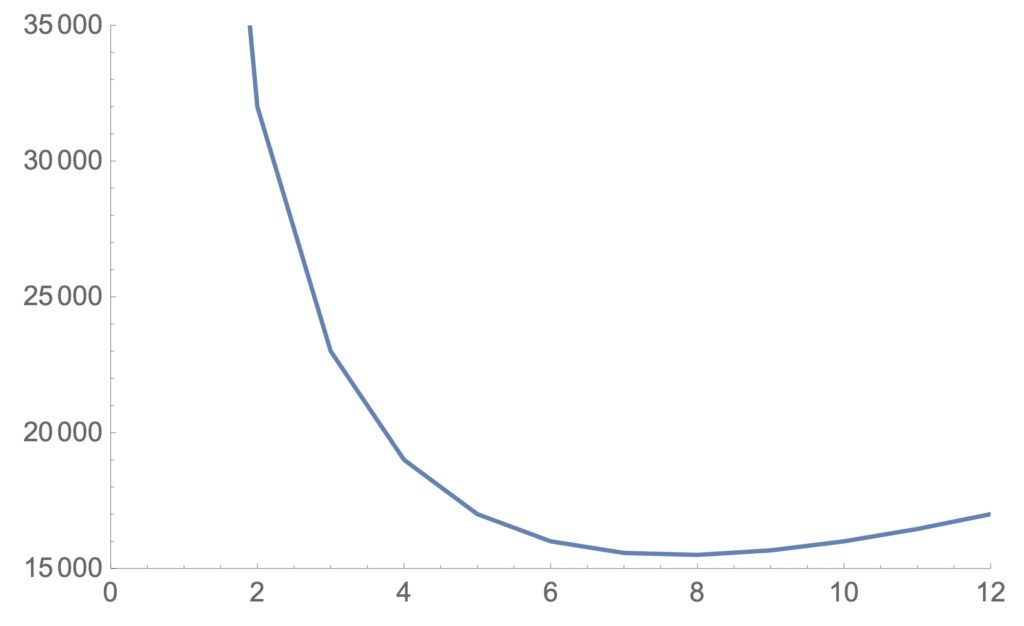
図2:発注回数と年経費の関係
この場合、k=8、つまり、年間8回注文するのが最適であり、注文量は2400/8=300です。
2.2 発注点
発注点を計算する場合、考慮すべき事項は、需要のバラツキと調達期間のバラツキです。従って、発注点は調達期間中の平均需要量に安全余裕を加えたもので、次のように式で表されます。
ここで、K:発注点

a:安全係数
Sd:時間単位の需要のバラツキ
なお、ここで不足の確率に応じる安全係数は次の通りです。
表1:不足の確率に応じる安全係数
| 不足の確率 | 1% | 2.5% | 5% | 10% | 15% |
| aの値 | 2.33 | 1.95 | 1.65 | 1.28 | 1.04 |
次に最大調達期間が2カ月、過去6カ月の需要量が下の表で与えられています。このときの発注点を求めてみたい。このとき、安全係数は1.95とします。
表2:過去6カ月の需要量
| 月 | 1 | 2 | 3 | 4 | 5 | 6 |
| 需要量 | 327 | 350 | 342 | 336 | 318 | 347 |
<<リスト3>>
n=6;
d={327,350,342,336,318,347};
de=Apply[Plus,d]/n;(*平均*)
s=Sqrt[Apply[Plus,d*d]/n-de*de];(*分散*)
Print[“需要平均=“,N[de]];
Print[“需要のバラツキ=“,N[s]];
需要平均=336.667
需要のバラツキ=11.22
k[t_,d_,a_,s_]:=N[t*d+a*Sqrt[t]*s](*発注点の公式*)
a=1.95;(*安全係数*)
t=2;(*最大調達期間*)
k[t,de,a,s]
704.275
2.3 応用例
(1)購入数量により単価の値引きがある場合の最適発注量
大量に購入した場合に値引きが行なわれることがあります。このような場合の最適発注量を考えます。
表3:購入数量による値引き
| 購入数量 | 単価(円) | 割引 |
| 0〜3000 | 150 | なし |
| 3000以上 | 120 | 2割 |
年間使用量r15000、発注費c1回3000円、保管費率p20%とします。
当然、年間に掛かる在庫の経費を最小限にすることが最適の条件です。
在庫の経費=年間在庫保管費用+年間注文費用です。
kを年間の注文回数とすると在庫の経費は、yc[r_,c_,p_,n_,k_]:=r/k/2.*p*n + c*kで表わされます。
リストにより、年間の注文回数を1〜12まで変化させてプロットさせたものを図3に示しました。
なお、15000/3000=5回以下の発注の場合には単価が120円です。
<<リスト4>>
a=Table[{i,If[i>5,yc[15000,3000,150,.20,i],
yc[15000,3000,120,.20,i]]},{i,1,12}];(*経費の計算*)
Print[a];(*結果のプリント*)
ListPlot[a,PlotJoined->True](*グラフ表示*)
{{1, 183000.}, {2, 96000.}, {3, 69000.}, {4, 57000.},
{5, 51000.}, {6, 55500.}, {7, 53142.9}, {8, 52125.},
{9, 52000.}, {10, 52500.}, {11, 53454.5}, {12, 54750.}}
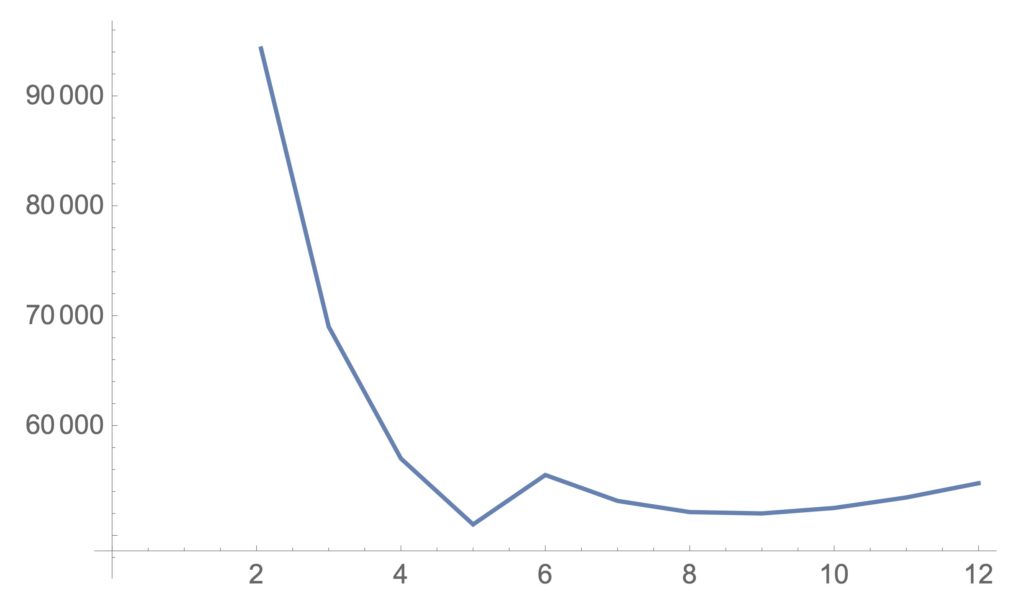
図3:注文回数と年間経費
図3及び年間経費の値から5回で3000個以上注文するのが有利であることが分かります。
(2)調達期間がばらつく場合の発注点
調達期間がばらつき、過去のデータから最大調達期間を決定することが困難な場合、過去のデータから調達期間を決定しなければなリません。
ここで、最大調達期間を過去のデータから次のように決定します。
T=To+a St
ここで、T:最大調達期間
To:平均調達期間
a:安全係数
St:調達期間のバラツキ
上の式を発注点を求める式に代入すると次のようになる。

Sd:時間単位の需要のバラツキ
なお、ここで安全係数は通常の場合よりも小さくしても構いません。なぜならば、需要も調達期間も共に安全係数をかけており需要が多く調達期間が延びることが同時に起こらなければ在庫切れ等が起こることはないからです。
1節で行なったシミュレーションを調達期間もばらつく場合に書き直し、安全係数が小さい場合の在庫切れの起こり易さをシミュレーションしてみます。
ここでは、調達期間は l1minから l1maxまで一様分布するものと考えます。
<<リスト5>>
nmlrnd[e_,std_]:=N[e+std*Cos[2 Pi Random[]]*
Sqrt[-2 Log[Random[]]]]
inventory2[e1_,s1_,i0_,i1_,o1_,l1min_,l1max_,l2_]:=
Block[ {l=0,i=i0,a={i0},of=0,l3},
While[l<l2,l++;
i=i-Round[Abs[nmlrnd[e1,s1]]];
If[i<=o1 && of==0,of=1;l3=l+Random[Integer,{l1min,l1max}],];
If[of==1 && l3<=l,i=i+i1;of=0, ];
a=Append[a,i];
];
ListPlot[a,PlotJoined->True];
]
「ある店屋が、当初23の在庫を持っています。徐々に売れていき、7になったとき問屋に発注します。発注してから2日〜4日(一様分布)が経ってから注文した30が到着しそれを元にまた商売を続けていきます。そして、平均3及び標準偏差1の正規分布に従う売れ方をしているものとしています。」の場合を考えてみると、inventory2[3,1,23,30,7,2,4,50]でシミュレーションを実施できます。
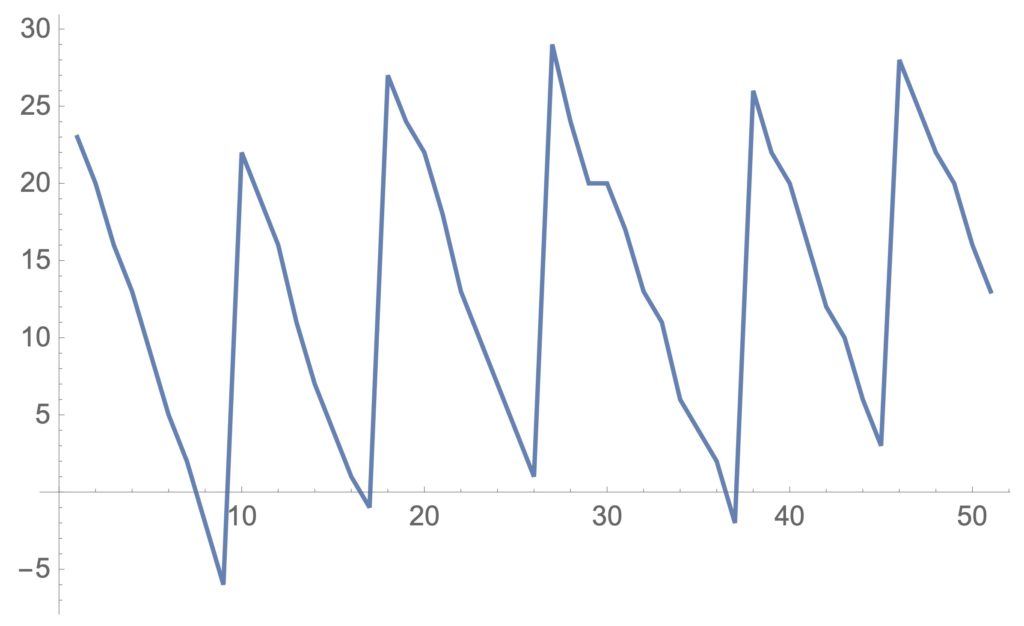
図4:調達期間もばらつく場合
何度か実行してみると調達期間が一定の場合と同じ発注点では、在庫切れが起こっていることが分かります。
3 定期発注法
定期発注法は発注点法と比較すると、取扱う品物の需要の変動も金額も大きい場合に、あらかじめ発注時期が決め、より正確な在庫管理を行なうために用いられます。
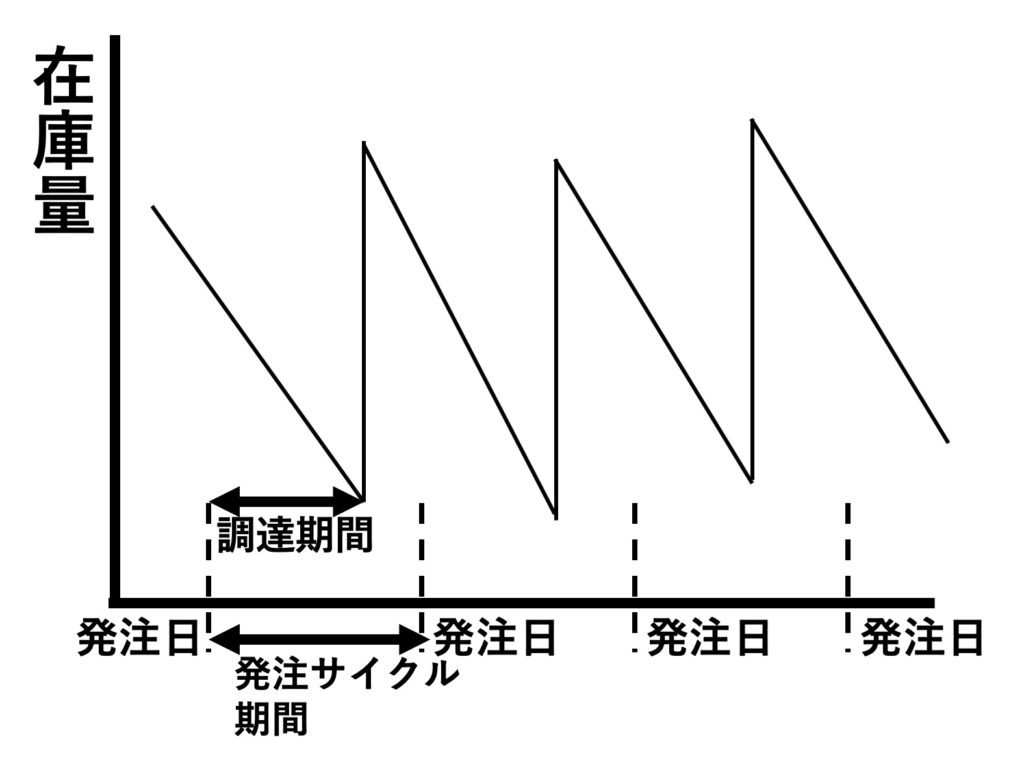
図5:定期発注法の発注間隔
定期発注法において、あらかじめ決められた発注間隔のことを発注サイクル期間と呼んでいます。発注して需要に応じられる間での期間を調達期間と呼ぶのは、発注点法と同様です。
3.1 発注量の決定
定期発注法における発注量は次の式で表されます。

L:現在の発注残
E:現在の在庫量
S:安全余裕
需要量の推定については、4章を参照してください。
3.2 発注サイクル期間の決定
定期発注法においても経済的に運用するためには、発注点法と同様に保管費用と発注費のバランスが取れた経済的な発注量で発注する事が望ましい。
例えば、最適発注量が1500であり、月間の平均需要が500である場合には、1500/500=3カ月を発注サイクル期間とすることが望ましいわけです。
式で示すと次のようになります。
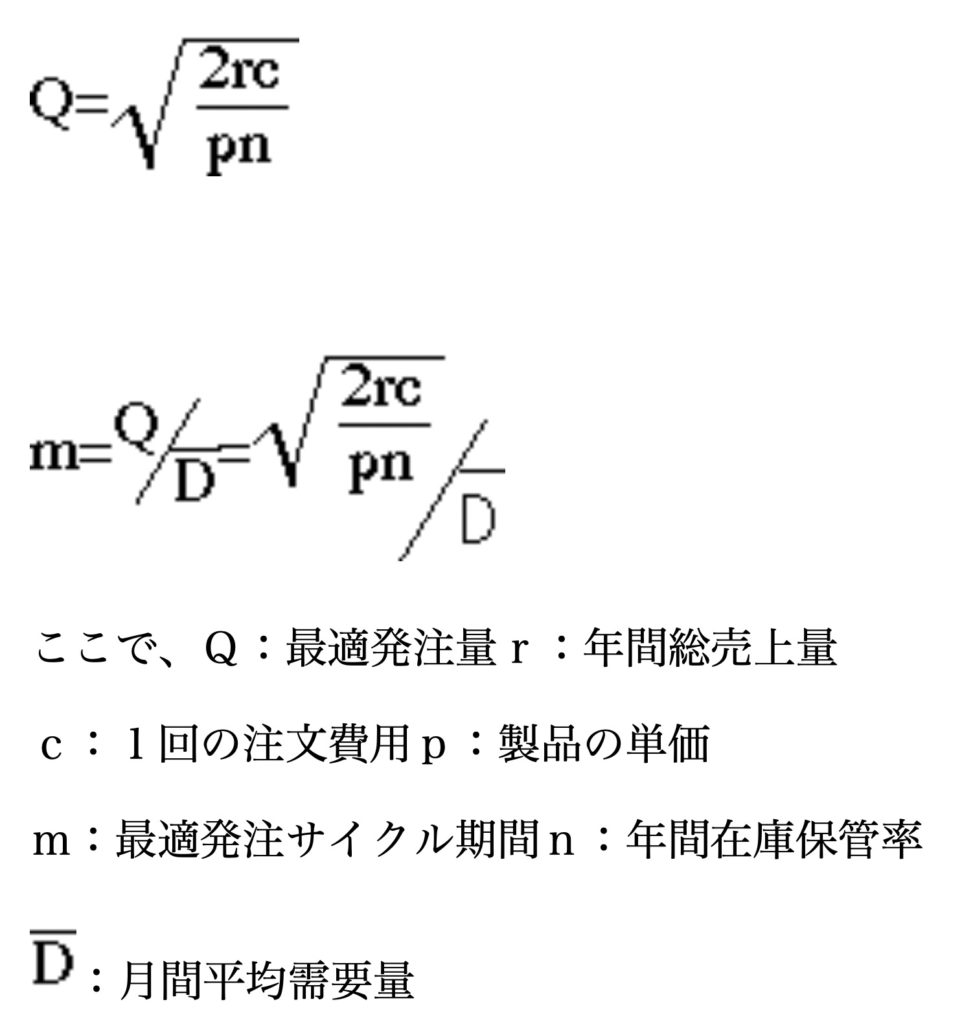
年間総売上量を15000、1回の注文費用3000円、製品の単価120円、年間在庫保管率20%、月間平均需要量を1240とすると、最適発注サイクル期間は、次で求めることができます。
m[r_,c_,p_,n_,d_]:=Sqrt[2*r*c/(p*n)]/d
m[15000,3000,.2,120,1240]
1.56169
3.3 安全余裕の決定
安全余裕は、推定需要量より実際の需要量が大きい場合に不足が起こらないように用意しておく在庫です。
(1)月間需要量から求める場合
需要の実績値のデータしかない場合には、次の式で安全余裕SLを求めます。
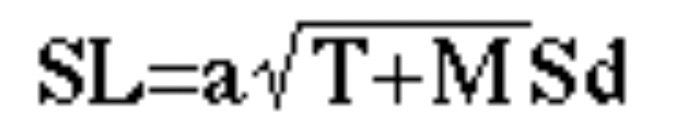
ここで、T:調達期間
M:発注サイクル期間
a:安全係数
Sd:時間単位の需要のバラツキ
安全係数は、当初、2くらいを用い、しだいに少なくして行くべきでしょう。なぜならば、上の式はTとMの期間が大きければ安全余裕が非常に大きくなるからです。また、推定値と実績値のデータを得るに従って、下の方法に移行して行くべきです。
過去6カ月の需要が下表にあるとおりでした。調達期間1カ月、発注サイクル3カ月、安全係数を2として安全余裕を求めてみよう。
表4:過去6カ月の需要
| 月 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
| 需要量 | 330 | 390 | 270 | 280 | 310 | 350 |
<<リスト6>>
saftylevel[a_,t_,m_,std_]:=N[a*std*Sqrt[t+m]](*安全余裕の公式*)
demmand={330,390,270,280,310,350};(*需要データ*)
n=Length[demmand](*データ数*)
6
mean=N[Apply[Plus,demmand]/n](*需要の平均*)
321.667
sigmma=N[Sqrt[Apply[Plus,(demmand-mean)^2]/n]](*需要の標準偏差*)
40.9946
saftylevel[2,1,3,sigmma](*安全余裕の算定*)
163.978
もし、ここで発注サイクル期間を1カ月にすると、
saftylevel[2,1,1,sigmma](*安全余裕の算定*)
115.95
安全余裕が、約50減ることになります。このように在庫を減らすには発注サイクル期間を短くすることが有意義です。
(2)過去の推定値と実績値のデータがある場合
過去の推定値と実績値のデータがある場合には、その差のバラツキから安全余裕を求めることができます。
調達期間1カ月、発注サイクル期間2カ月の場合に需要の推定値と実績値を次のように得ました。
表5:需要の推定値と実績値
| 1〜3月 | 2〜4月 | 3〜5月 | 4〜6月 | 5〜7月 | 6〜8月 | 7〜9月 | |
| 推定値 | 1640 | 1520 | 1500 | 1460 | 1540 | 1600 | 1660 |
| 実績値 | 1587 | 1486 | 1462 | 1525 | 1564 | 1633 | 1618 |
| 差 | 53 | 34 | 38 | -65 | -24 | -33 | 42 |
<<リスト7>>
demmand2={53,34,38,-65,-24,-33,42};(*ばらつきのデータ*)
n=Length[demmand2](*データ数*)
7
mean=N[Apply[Plus,demmand2]/n](*ばらつきの平均*)
6.42857
sigmma=Sqrt[Apply[Plus,(demmand2-mean)^2]/n] (*ばらつきの標準偏差*)
42.7179
2.5%(片側)の安全余裕を取るのであれば、1.96を乗じればよい。
1.96*sigmma
83.727
なお、この場合の安全余裕は推定の誤差分だけをまかなうのであるから、需要が変化しても変更する必要はありません。その分が需要の推定量の中に入っていると考えられます。
参考文献
1 水野 幸男 OR ライブラリー9「在庫管理入門」日科技連
2 中村健蔵2019『MathematicaによるOR』楽天Kobo・キンドルDP
ノートブックのダウンロードについて
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。