要旨:MBA取得のためのMathematica 5としてシミュレーションの基本・本質を把握してもらえるようにπの算定を例にして解説する。
なお、ノートブックのダウンロードについては末尾から出来ます。
1 シミュレーションとは
シミュレーションとは、ある対象について模型(モデル)を作り、まねることです。その目的は、いろいろなことが考えられますが、例えば、費用が掛かるからであったり、人命に関することであったり、手軽に何度もやってみるためであり、より簡単に行なえるようにするものです。現在、計算機が発達し、その中で簡単に各種モデル、特に数学モデルを容易に組み立て実行できるので、シミュレーションが計算機上で利用されることになります。
本書においても、シミュレーションを重要なものと考えています。その理由は、
(1)ORにおいて登場する問題の多くは、あまりにも複雑であって、容易に数学的形式化ができない場合、できても数学的に解答を求めることが困難な場合が多い。このような場合でも、一部分を捉える、もしくは簡略化することにより、決定論的又は確率的問題の如何を問わずシミュレーションを使って解答が求めることができます。
(2)求めた解の妥当性と限界を検証することができます。
(3)いろいろな現象についての理解を容易にする効果があります。つまり、前にも述べた様にシミュレーションを通じて、そのモデルなり、現象なりを体験することができ、理解を促進すると共に、結果を視覚化するものと考えています。また、ORワーカーとしては、説得のための一方法として活用できます。
ところで、シミュレーションと言うとモンテカルロ型シミュレーションのことと考える人もいるようです。確かにシミュレーション手法のうちでもっとも代表的なものですが、この手法の特徴は乱数発生により、計算機上の数値計算にすることによって解答を求める点にあります。一般にシミュレーション手法による問題解決の中には必ずしも、乱数を使わないものもあり、この点でシミュレーション手法の方がモンテカルロ法より広い意味になります。とは言っても、ORにおいて登場する問題の多くは、複雑であり、確率的な変数が入る場合が多いことは事実です。従って、以下、確率的なシミュレーションを主に述べます。
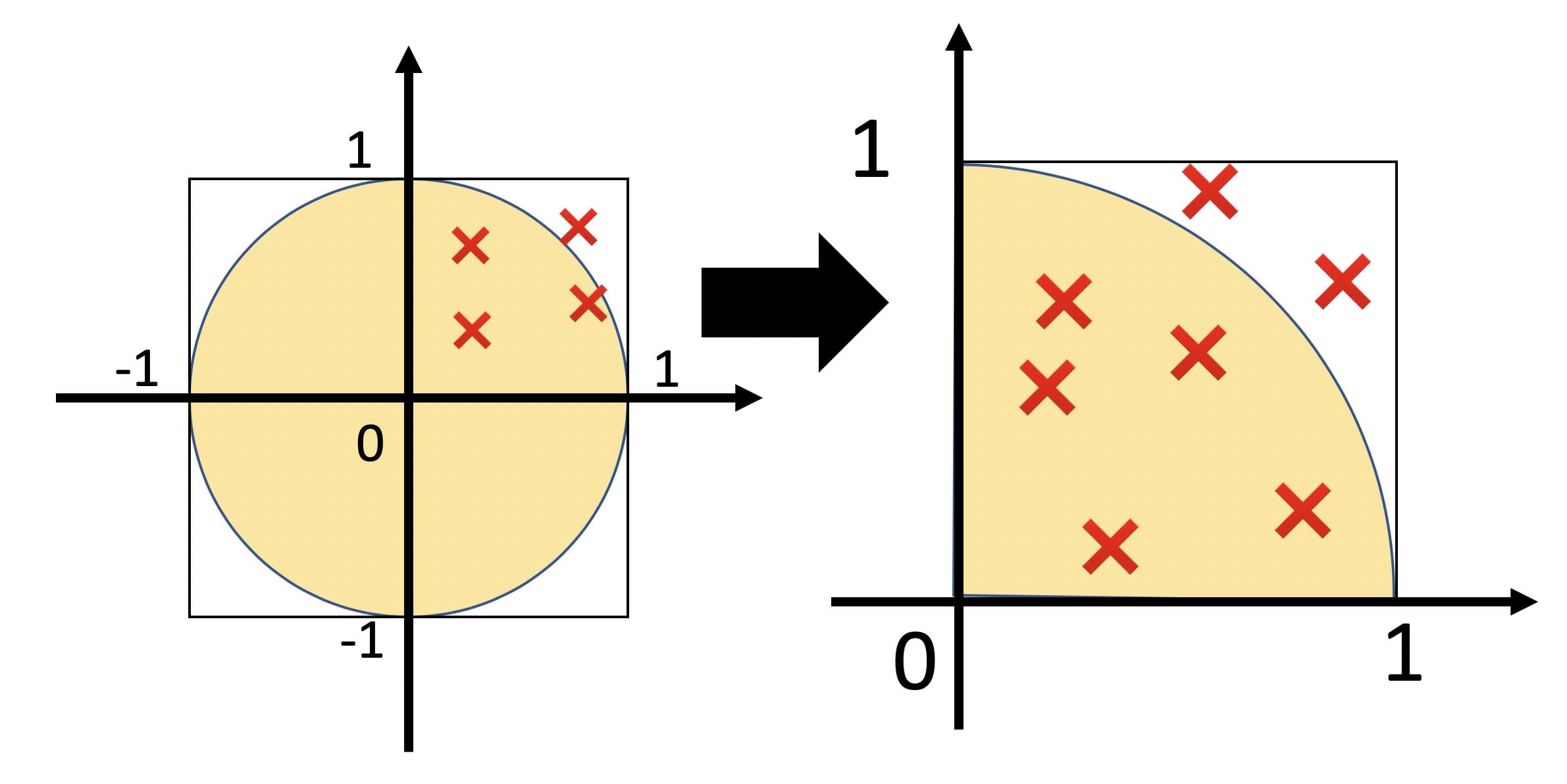
モンテカルロ法の簡単なシミュレーションの一例としてπの値の計算を試みます。方法は簡単で、図1に示すように半径1の円は面積がπです。また、円が内接する四角形の面積は4です。従って、面積の比率はπ/4となります。このことからx及びyの2つの一様乱数を発生させ、円の中に入るかはいらないかを判定し、その比率からπの値の近似値を得ようとするわけです。
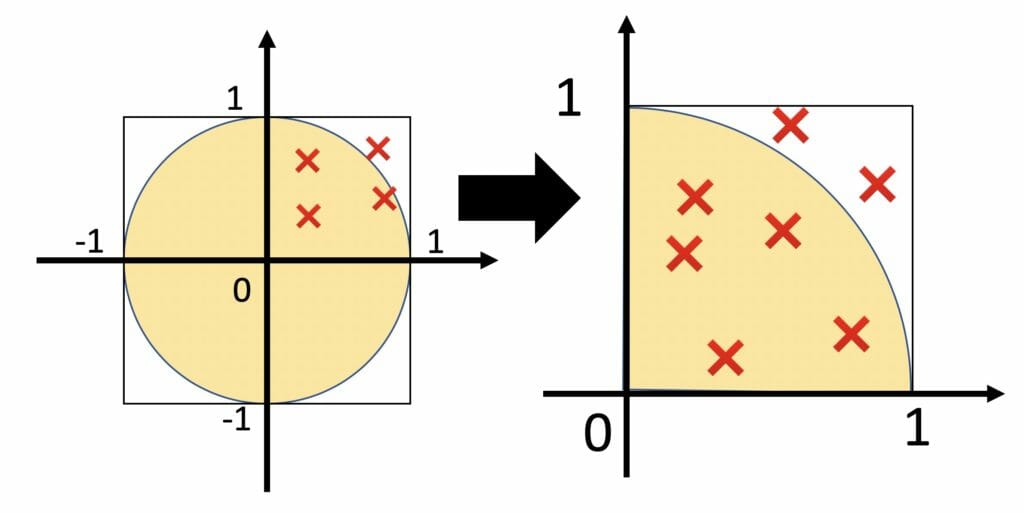
図1:πの求め方の概念図
プログラムはsimpi[シミュレーションの回数]により100回毎のπの値と分散をグラフに表示するようになっています。なお、実際のプログラムは全体ではなく、第1象限のみを考え、それを4倍することによりπを求めています。 シミュレーションの精度については、後ほど述べますが、グラフから収束があまり早くないことが分かります。
simpi[n_] :=
Module[{i = 0, k = 0, pi, s = 0, v = 0, a = {}, b = {}},
While[i < n, i++;
If[Random[]^2 + Random[]^2 > 1, , k++];
pi = N[4*k/i];
s = N[s + pi];
v = N[v + pi*pi];
If[IntegerQ[i/100], d = Sqrt[v – s*s/i/i]/i;
Print[i, ” “, pi, ” “, d];
a = Append[a, {i, pi}];
b = Append[b, {i, d}],]] ;
GraphicsColumn[{ListPlot[a, PlotJoined -> True, PlotRange -> {2.8, 3.4}],
ListPlot[b, PlotJoined -> True, PlotRange -> {0, 0.2}]}]]
simpi[3000]
100 2.96 0.280442
200 3.1 0.208147
300 3.21333 0.17387
400 3.16 0.152966
500 3.192 0.137903
600 3.18667 0.126535
700 3.18857 0.117643
800 3.175 0.110365
900 3.17778 0.104303
1000 3.152 0.0990736
1100 3.15273 0.0945265
1200 3.16333 0.090558
1300 3.15385 0.0870483
1400 3.16286 0.0839168
1500 3.16 0.081108
1600 3.1675 0.0785706
1700 3.17176 0.0762675
1800 3.16222 0.0741505
1900 3.15368 0.0721885
2000 3.156 0.0703667
2100 3.15048 0.0686824
2200 3.14909 0.0671023
2300 3.14609 0.0656268
2400 3.14333 0.0642452
2500 3.1472 0.0629447
2600 3.14769 0.0617224
2700 3.15407 0.0605712
2800 3.14857 0.0594836
2900 3.15034 0.0584501
3000 3.15467 0.0574713
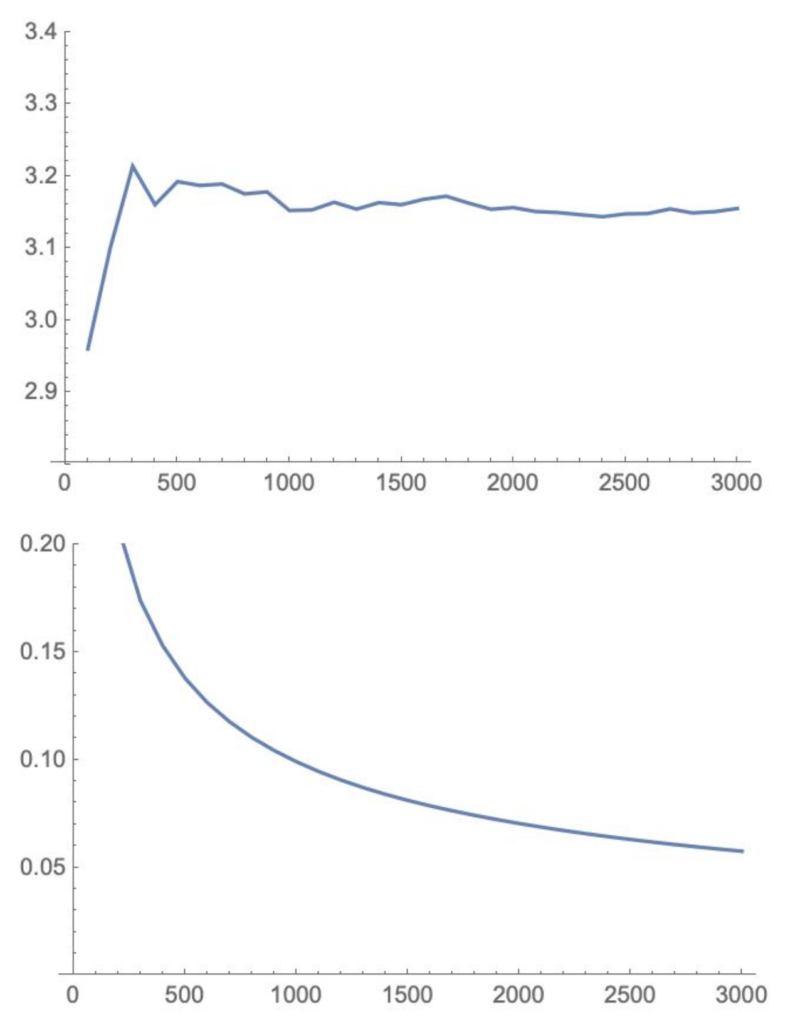
図2 シミュレーションの回数とπの値(上図)
図3 シミュレーションの回数と標準偏差の収束
以下、各種乱数の発生方法及び使い方と応用例及び精度について述べます。
2 乱数の発生と検定
2.1 乱数(Random Digits)
例えば、標本を抽出する際、偏りのあるものでは困るので、何らかのやり方で、等確率で出鱈目になるように選んだ数字の列が使用されます。この数字の列を乱数列、又は乱数と呼びます。従って、乱数とは0から9までの数字が等確率、即ち1/10であらわれる数列ということになっていました。
その後、統計・確率の発展と共に、乱数にも、数字が等確率であらわれる一様乱数とある確率密度に従い数字があらわれる特殊乱数が使われるようになります。特殊乱数の代表的なものには正規乱数、指数乱数、ポアソン乱数などがあります。また、出てくる数字が整数等の離散型の離散型乱数と連続な連続型乱数があります。
2.2 一様乱数の発生
0から9までの数字が等確率、即ち1/10であらわれる数列、即ち、最も歴史的な意味での一様乱数を得る方法には、サイコロやルーレット等の乱数器及び乱数表の使用が考えられます。
計算機において上記のものを利用するには簡単さと大量のものを得る点で問題があります。また、シミュレーションで用いるためには、等確率で出鱈目であることの他に、さらに再現性:必要に応じ同じ乱数列をいつでも発生させられることが要求されます。なお、出鱈目であること(無周期性)については、十分に長い周期であれば実用上は問題ないと思われます。
計算機で乱数を発生させる方法には、フォン・ノイマンの考案になるといわれる平方採中法や各種合同法などがあります。ここでは合同法の2種類について紹介します。
(1)合同法 I(レーマー法又は乗算合同法)
合同式Xn+1=k Xn(mod M)によって、乱数列を作り出す。k、M及びXoを何にするかによって、簡単に乱数列を変更することができます。
ここで、k=23、M=10^8+1としたときの周期は5882352です。
この方法で[0、1]の一様乱数列を得るプログラムは、再帰的に書くと
f[0]=xo;
f[i_]:=f[i]=Mod[k f[i-1],m];
k=23;
m=10^8+1;
xo=1;
n=10;
Table[N[f[i]/m],{i,n}]
{2.3*10^-7, 5.29*10^-6, 0.00012167, 0.00279841, 0.0643634, 0.480359, 0.0482541, 0.109845, 0.526435, 0.107994}
理解しやすいが、メモリを多く使用するので手続き型で書き直すと
ran1[k_,m_,xo_,n_]:=
Module[{ran=xo,a={},i},
For[i=1,i<=n,i++,
ran=Mod[k ran,m];
a=Append[a,ran/m]
];
a//N
]
ran1[23,10^8+1,1,10]
{2.3*10^-7, 5.29*10^-6, 0.00012167, 0.00279841, 0.0643634, 0.480359, 0.0482541, 0.109845, 0.526435, 0.107994}
(2)合同法 II
Xn+2=Xn+1+Xn(mod M)で乱数列を得るものです。
ここで、M=2^44とすれば、周期は3×2^43、つまり、
約2.5×10^13です。
Clear[f];
m = 2^44;
xo = 2^22 + 1;
x1 = 2^23 + 1;
f[0] = xo;
f[1] = x1;
f[i_] := f[i] = Mod[f[i – 1] + f[i – 2], m];
n = 100;
Table[N[f[i]/m], {i, n}]
これもメモリを多く使用するので手続き型で書き直すと
ran2[m_,xo_,x1_,n_]:=
Module[{ran0=xo,ran1=x1,a={},i=1},
While[i<n,i++;
ran=Mod[ran0 + ran1,m];
ran0=ran1;
ran1=ran;
a=Append[a,N[ran/m]]
];
a
]
a=ran2[2^44, 2^22 + 1, 2^23 + 1,100]
(3)Mathematicaにおける乱数の使い方
Mathematicaにおいて乱数を使用する場合、組み込み関数で一様乱数を発生させることができ、それを使用することが使いやすさにおいても速度においても最も有利と思われるので、使い方について述べます。
Random[] 区間(0、1)の実数の乱数
Random[Real,xmax] 区間(0、xmax)の実数の乱数
Random[Real,{xmin,xmax}] 区間(xmin、xmax)の実数の乱数
Random[Complex,{zmin,zmax}] 矩形(zmin,zmax)の複素数の乱数
Random[Integer] 1と0を確率1/2で発生する乱数
Random[Integer,{imin,imax}] 区間(imin、imax)の整数値の乱数
n桁の精度で乱数を発生させたい場合には、
Random[type,range,n] という記法で書けばよい。
乱数列を変更したい場合には、
SeedRandom[] 日付と時刻により新しいシードを与える。
SeedRandom[s] 整数sでシードを与える。従って、再現性をもたせたい場合には、この関数を使用します。
2.3 一様乱数の検定
一様乱数の検定には、次のようなものがあり、その概要を示します。
(1)頻度検定
出現の等確率性をχ2検定するものです。
例えば、0から9までの整数の乱数100個についてχ2検定する場合には、次のようになります。
n=100; (*発生個数*)
e=n/10; (*発生の理論度数*)
a=Table[Random[Integer,{0,9}],{n}]; (*乱数列の発生*)
b=Table[Count[a,i],{i,0,9}]-e; (*数を数えて、理論度数を引く*)
c=N[Apply[Plus,b^2/e]] (*χ2値の算定*)
11.8
自由度は10ー1=9で、有意水準5%とすれば、χ2o=16.919となります。従って、この乱数は頻度に差があるとはいえません。なお、有意水準10%とすれば、χ2o=14.68となります。上の例では、乱数は頻度に差があるとはいえませんが、何度かやると差があるという場合もでてきます。
(2)継次検定
0〜9までの乱数を発生させ、数字を1個ずつずらしながら続きの2個の乱数の出現の等確率性をχ2検定するものです。これは、0〜99までの乱数を発生させ、頻度検定を行った場合とは異なり、ある数字の次に出てくる数字に偏りがないかを検定しています。
00から99までの100通りの組み合わせの出現確率が1/100であることから(1)と同様の手順で検定できます。
(3)ポーカー検定
ランダムな数字の列から数字を1個ずつずらしながら連続する5個の乱数の組を取りだし、それらがポーカーゲームの「ファイブ・カード」「フォー・カード」「フルハウス」「スリーカード」「ツウペア」「ワンペア」等の役になる組み合わせになっているかどうかを調べ、理論的出現頻度との間にχ2検定を行なうものです。
役の出現確率(10000回における理論度数)
「ファイブ・カード」 1
「フォー・カード」 45
「フルハウス」 90
「スリーカード」 720
「ツウペア」 1080
「ワンペア」 5040
「役なし」 3024
(4)ギャップ検定
数列中の1つの数字に注目し、その数字がどれだけの間隔をもって現われるかを調べます。
3 確率分布に従う乱数(特殊乱数)の作り方
計算機上でのシミュレーションのためのモデルでは、いろいろな確率分布に従う乱数が利用されます。従って、それらに従う乱数を発生させることが必要となります。Mathematicaにおいて、各種特殊乱数を発生させる方法について述べます。
その方法を一般的な形で言うと、下図にあるように累積確率分布関数
y=F(x)の逆関数x=F-1(y)を使用し、[0,1]の範囲の一様乱数の写像を得ればよいわけです。
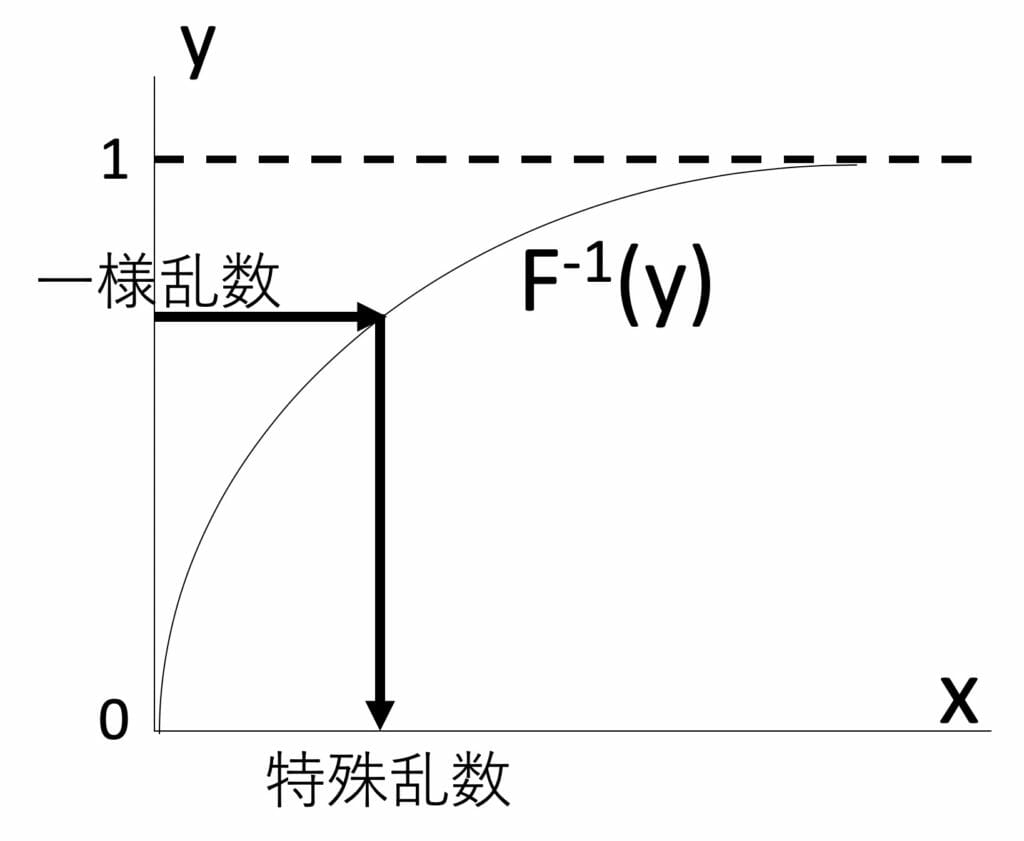
図4:特殊乱数の作り方
しかしながら、この方法では、累積確率分布関数が解析的に求められていないものや効率的でないものもあるので、それらについても説明します。
3.1 離散型分布
(1)ベルヌーイ分布(Bernoulli Distribution)
成功の確率をpとし、結果xを成功の場合1、失敗の場合0とするとき、変数xの分布を確率pに基づくベルヌーイ分布といいます。
bdran[p_]:=If[p<Random[],0,1]
100個の乱数を発生させ、その時の成功の確率を表示させます。
n=1000; (*乱数の個数*)
p=0.1; (*成功の確率*)
a=Table[bdran[p],{n}]; (*n個の乱数を発生*)
b=N[Count[a,1]/n] (*成功率*)
0.081
(2)2項分布(Binomial Distribution)
ベルヌーイ試行を連続してn回行なった場合、x回成功する確率は、
P(x)=nCx p^x(1ーp)^(n-x)で示されます。この時、確率変数xの分布を2項分布といいます。
ベルヌーイ分布の乱数を使用して幾何分布の乱数を発生させると
biran[n_,p_]:=Count[Table[bdran[p],{n}],1]
ベルヌーイ分布の乱数を使用しない場合には、次のようになります。
biran[n_,p_]:=Count[Table[If[p<Random[],0,1],{n}],1]
(3)幾何分布(Geometric Distribution)
ベルヌーイ試行を連続して行なった場合、x+1回目に初めて成功する確率は、P(x)=p(1ーp)^xで示されます。この時、確率変数xの分布を幾何分布といいます。
ベルヌーイ分布の乱数を使用して幾何分布の乱数を発生させると
gdran[p_]:=
Module[{i=0},
While[bdran[p]==0,i++];i]
n=10;
p=.2005;
Table[gdran[p],{n}]
{7, 0, 1, 1, 1, 2, 3, 7, 1, 2}
(4)超幾何分布(Hypergeometric Distribution)
確率の所でも説明したように総数n個の母集団の中にm種類のものがあり、それぞれの個数はn1、n2、・・・nmです。この中からk個を取り出したとき、それぞれがk1、k2、・・・kmの場合の確率は、
p=n1Ck1 n2Ck2・・・nmCkm /nCk
で表されます。
このような確率分布を超幾何分布といいますが、この分布で最も利用されるのは2種類のものがある場合です。従って、母集団の総数n、特定のものの母集団における個数n1、取り出す標本の個数kの場合において、特定のものが取り出される個数xを乱数として発生させます。
hypran[n_,n1_,k_]:=
Module[{i=n+1,i1=n1,a={},h},
While[i>=n-k+2,i=i-1;
h=bdran[i1/i];
(*Print[i,” “,i1,” “,h];*)
If[h==1,i1=i1-1,];
a=Append[a,h];
];
Count[a,1]
]
Table[hypran[200,80,40],{10}]
{13, 12, 17, 23, 17, 16, 13, 18, 17, 13}
上では、例えば赤黒の玉が合計200個、赤玉は80個あり、取り出して戻すことを40回繰り返した場合の赤玉の個数は幾つになるかを10回表示しています。
(5)ポアソン分布(Poisson Distribution)
事象が時間的にランダム(事象の発生時間間隔が指数分布に従う)に発生する時、単位時間内に事象がx回発生する確率P(x)は次の式で表されます。
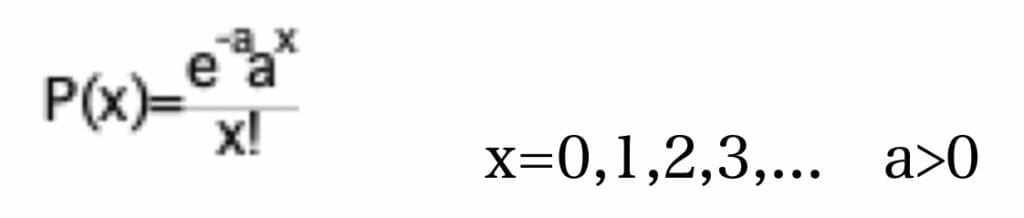
ここで、aは単位時間内の事象の平均発生回数です。
この分布をポアソン分布といいます。待ち行列における客の単位時間の到着数は、この分布に従う事が多く、現実でも単位時間の患者の病院への到着数や駅への列車の到着数等は、これに従うことが分かっています。
乱数の発生については、発生の時間間隔が指数分布に従う事を利用するのが、効率的です。
3.2 連続型分布
(1)正規分布(Normal Distribution)
最も良く知られた分布であり、シミュレーションにおいても最も利用範囲が広いと思われます。なぜならば、中心極限定理により同じ分布を持つn個の独立な確率変数xiの和は、それぞれの平均をei、分散をviとすれば、もとの分布が何であろうと、nの値が大きくなるに連れて、平均e=ei^2、分散v=vi^2 をもつ正規分布に近づくからです。
従って、一様分布を12個足すことによって、正規分布を得ることができます。この時の平均は6、及び分散は1/12*12=1です。これをプログラムにすると
nmlrnd1[e_,s_]:=N[e+s*(Sum[Random[],{i,12}]-6)]
Table[nmlrnd1[0,1],{100}]
正規分布は、より直接的に2個の一様乱数を用いて作ることができます。この方法については、公式のみが記述されることが多いようですので、公式の導出について若干触れてみます。
標準正規分布に従う独立な2変数x、yを考える。この同時確率分布密度関数は次式で表されます。
x、y〜N(0、1)
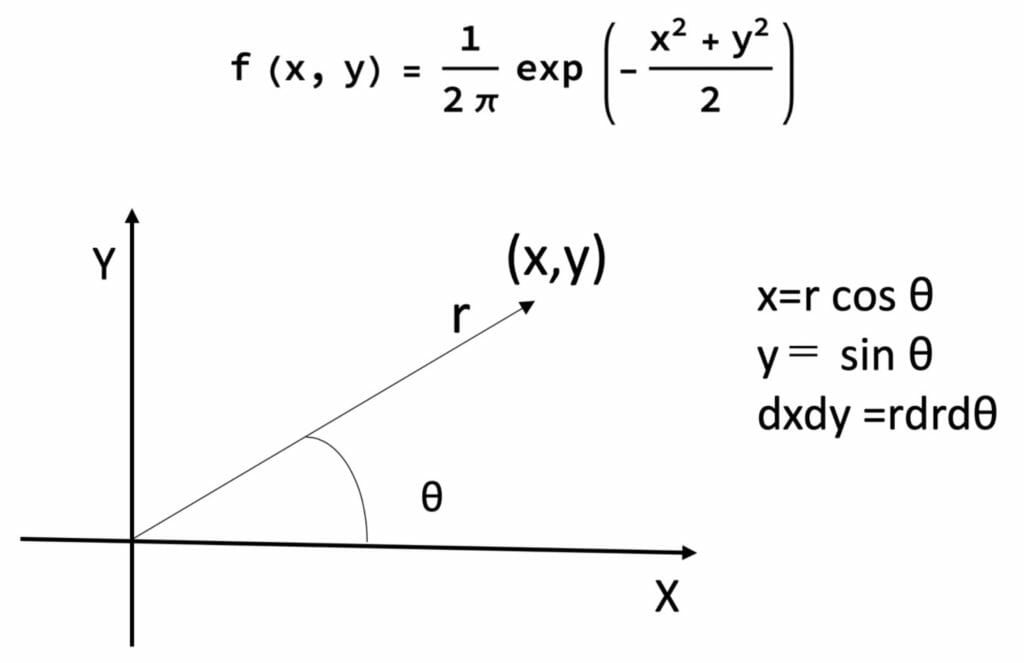
図5:正規乱数を作るための局座標変換
これを曲座標変換するとその確率分布関数を求める事ができます。
F(r,θ)=1-exp(-r^2/2)
原理的な説明としては、この分布関数を利用して1個の一様乱数からrを求め、さらにもう1個の一様乱数でθの値を決めxとyに分解するものと考えればよいわけです。つまり、これをx、yに逆変換することで公式が求まります。
これにより2個の一様乱数(u,v) を用いて、2個の独立な正規乱数x、yを作る事ができます。
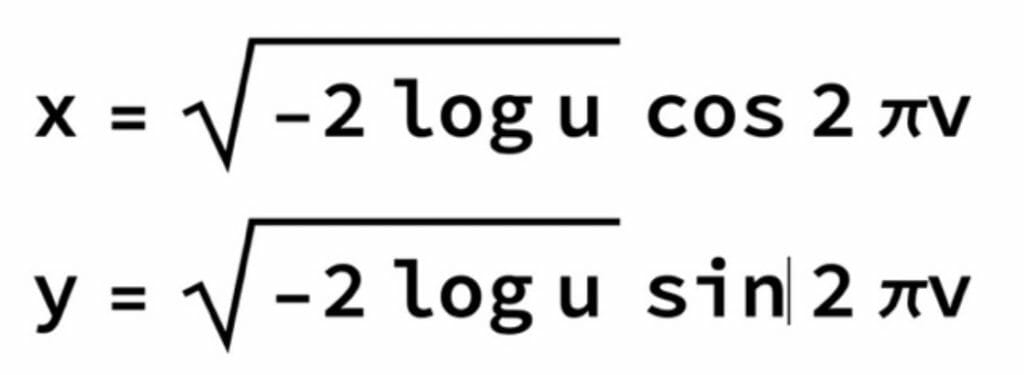
従って、この公式を用いることによって、正確に乱数を発生させることができることが分かります。
nmlrnd[e_,std_]:=N[e+std*Cos[2 Pi Random[]]*Sqrt[-2 Log[Random[]]]]
Table[nmlrnd[0,1],{100}]
(2)対数正規分布(Lognormal Distribution)
対数を取ったものが正規分布に従う場合、もとの変数の分布を対数正規分布といいます。この分布は、所得や会社の資本金の分布として現実によく現われる分布型です。
乱数の発生法は、変数xの対数log xが平均e、標準偏差sの正規分布に従っているので、正規乱数を変換することから発生させることができます。
対数正規分布の平均le、標準偏差lsとすると、正規分布の平均e、標準偏差sは次の式で表されます。
s2=log((ls/le)2+1)
e=logleーs2
この式を用いて乱数を発生させると次の通りです。
logrnd[le_,ls_]:=
Module[{e,s},
s=Log[(ls/le)^2+1];
e=Log[le]-s/2;
s=Sqrt[s];
N[Exp[nmlrnd[e,s]]]
]
Table[logrnd[5,1],{20}]
{4.04455, 5.46147, 3.99504, 5.27773, 6.62812, 4.16541,
4.69197, 6.17777, 4.91332, 4.80852, 4.27405, 5.62244,
4.56965, 6.41296, 3.79015, 5.36323, 4.83126, 6.09791,
6.09711, 6.28762}
(3)指数分布(Exponential Distribution)
ポアソン分布の所で述べたように、事象が時間的にランダムに発生する時、事象の発生時間間隔は、指数分布に従います。
この分布の乱数は、累積確率分布の逆関数を使って、発生させることができます。
累積確率分布関数 F(x)=1ーe-ax
逆関数 G(r)=ー1/a log(1-r)
なお、乱数を発生させるときには、1ーrもrも同じ分布です。従って、
exrnd[e_]:=-e*Log[Random[] ]
Table[exrnd[1],{20}]
{1.13269, 0.786786, 0.45059, 0.278257, 0.309677, 0.334169,
0.305071, 2.27557, 0.0524026, 4.1019, 2.9937, 3.68995,
0.812364, 0.0653578, 1.83935, 0.497893, 1.32776,
0.478777, 0.454858, 1.10725}
(4)アーラン分布(Erlang Distribution)
X0、X1、X2、X3、・・・Xnが独立で、全て同じパラメーターaの指数分布に従うとき、S=X0+X1+X2+X3+・・・+Xnをアーラン分布といいます。これは連続してn個の事象が発生する際の前経過時間の分布であると考えることができます。
従って、この乱数は指数分布に従う乱数から容易に発生させることができます。aを到着の平均時間間隔、nを事象の数とすると
erlrnd[a_,n_]:=
Module[{r=1},
Do[r=r*Random[],{i,n}];
-Log[r]/a
]
Table[erlrnd[1,5],{20}]
{1.62412, 3.28294, 3.89126, 4.87251, 4.92576, 9.17761,
4.45637, 4.58751, 5.85543, 2.46506, 6.25106, 4.88522,
6.50699, 5.14354, 6.41526, 5.3362, 4.67161, 3.58331,
4.7137, 6.20237}
(5)χ2分布(Chi-square Distribution)
自由度nのχ2分布は、標準正規分布に従う互いに独立なn個の変数の2乗和として得ることができます。 従って、正規乱数から発生させることができます。
chirnd[n_]:=Sum[nmlrnd[0,1]^2,{i,n}]
Table[chirnd[5],{20}]
{4.35331, 7.74392, 3.95565, 2.25862, 9.52434, 7.84459,
3.24058, 10.0093, 7.38077, 0.583158, 17.1226, 6.06004,
3.16005, 11.1434, 2.46253, 5.35135, 4.56362, 7.6976,
0.540649, 7.3486}
(6)F-分布(F-Diistribution)
自由度f1、f2のF-分布に従う乱数を求めるには、互いに独立で自由度
f1及びf2の2つのχ2分布に従う乱数の比を取ればよい。従って、次のようになります。
frnd[f1_,f2_]:=chirnd[f1]/chirnd[f2]
Table[frnd[3,5],{20}]
{0.738176, 2.01807, 0.401313, 0.261079, 0.173154,
0.421385, 0.164222, 0.22671, 1.02858, 0.452531,
0.510103, 1.62991, 0.128624, 1.26663, 1.31818, 0.759315,
0.161169, 1.04748, 0.123818, 0.803666}
(7)t-分布(t-Distribution)
t-分布に従う乱数は、F-分布とt-分布の関係から求めることができます。即ち、自由度nのt-分布の2乗は、自由度1、nのF-分布に従います。
trnd[n_]:=Sqrt[frnd[1,n]]*(1-2*Random[Integer])
Table[trnd[3],{20}]
{1.22521, 2.06766, -0.466102, 0.625298, 0.397877,
-2.77265, 0.129283, -0.558173, -0.386072, 0.638977,
-0.420009, 0.155859, 0.0239433, 0.0964505, 0.130735,
-1.37066, 0.0413153, 0.44207, -0.0168549, -0.565908}
4 シミュレーションの一例
シミュレーションとしてルーレットのシミュレーションを取り上げ、ルーレット必勝法について考えてみます。
ここで取り上げる必勝法は倍増法と呼ばれるものです。勝ったら賭けた分の倍戻しというギャンブルを考えて下さい。この時、賭ける側が、まず1単位の賭け金から始め、負たら賭け金を倍倍にし、勝ったら再度1単位の賭け金に戻して賭けを続けて行くという方法を倍増法といいます。

つまり、何回続けて負けても1回勝ったところで必ず1単位が、増えるようになっているわけです。
この方法で問題になるのは、次の2点です。
(1)資金をいくら用意するか。n回続けて負けても資金不足にならないためには、2^nー1単位以上を準備しておかなければならなりません。貧乏人の発想でいうと何回ぐらい続けて負けることがあると考えたほうがいいかということになります。これが分かれば、手持ちのお金から1単位とすべき賭け金が分かります。例えば、ラスベガスのルーレットの最小賭け金は最も安い所で1ドルです。もし、6回続けて負けて7回目の64ドルを出そうとすると総額127ドルの手持ちを準備しておく必要があります。
(2)1回勝っても1単位しか増えないので、何度も回数を掛けないと持ち金が増えないと予想されます。従って、例えば持ち金が倍に成るのに何回ぐらい賭けをする必要があるかが分かれば、好都合です。(持ち金が倍になれば、1単位の金額を倍にすることができます。)
4.1 ルーレット必勝法(その1)
ご存じのように、ルーレットとは黒・赤の0から36までの目に区分したすり鉢形円盤を高速度で回転させ、小さな球を投げ入れて、停止した時に球がどの目に止まるかを賭けて争うものです。上で説明した倍増法をルーレットで応用することを考えてみます。ルーレットで倍戻しのところといえば、偶数か奇数かを賭ける赤黒のどちらかに賭けるところです。従って、赤か黒かのどちらかに決めて、勝つまでは、その色に固定し賭け金を倍倍にしながら賭けていけばよいわけです。ただし、実際には0と00は親の総取りですから、勝つ確率は18/38=9/19であり、1/2よりやや小さい値となります。
それでは、ルーレットのシミュレーションを行なってみますが、まず手始めに持ち金がどのように変化するかを見てみることにします。リスト1では、roulette[持ち金、最小賭け金]で、持ち金が2倍又は無くなるまでの持ち金の変化をグラフで出力する関数を書いています。図6に関数の流れ図を示します。図7にSeedRandomの値を変えて、持ち金が2倍になった場合、無くなった場合、途中で回復してやっと2倍になった場合の持ち金の変化を示しています。なお、図の横軸が賭けの回数を、縦軸が持ち金を示しています。
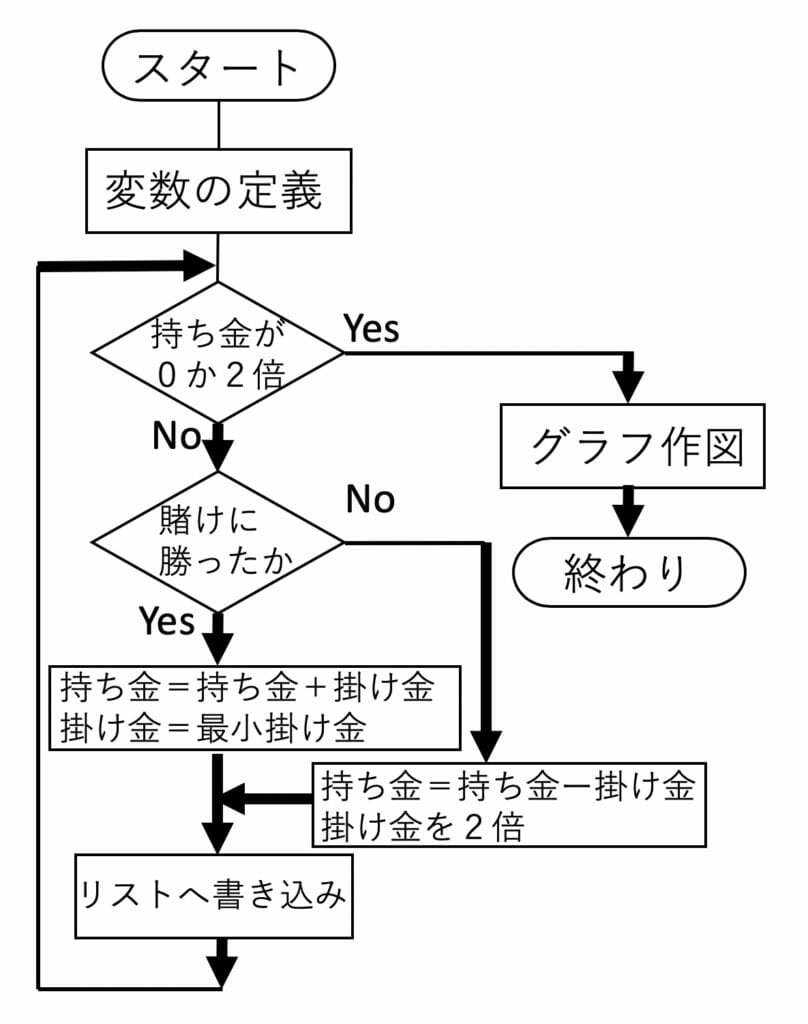
図6:流れ図(roulett)
<<リスト1>>
roulette[m0_,p0_]:= (*m0=持ち金,p0=最小掛け金*)
Module[{m=m0,n=0,p=p0,a={{0,m0}}}, (*変数の定義*)
While[m>0&&m<2 m0, n++; (*ループの設定*)
If[Random[]<=9/19,m+=p;p=p0,
m-=p;If[2 p>m,p=m,p=2 p]];(*乱数に応じる賭け金の操作*)
a=Append[a,{n,m}]; (*リストへの出力*)
];
ListPlot[a,PlotJoined->True,PlotRange->{0,2 m0}](*リストの作図*)
];
SeedRandom[1234567]; (*乱数列の初期化*)
roulette[100,1] (*関数の実行*)
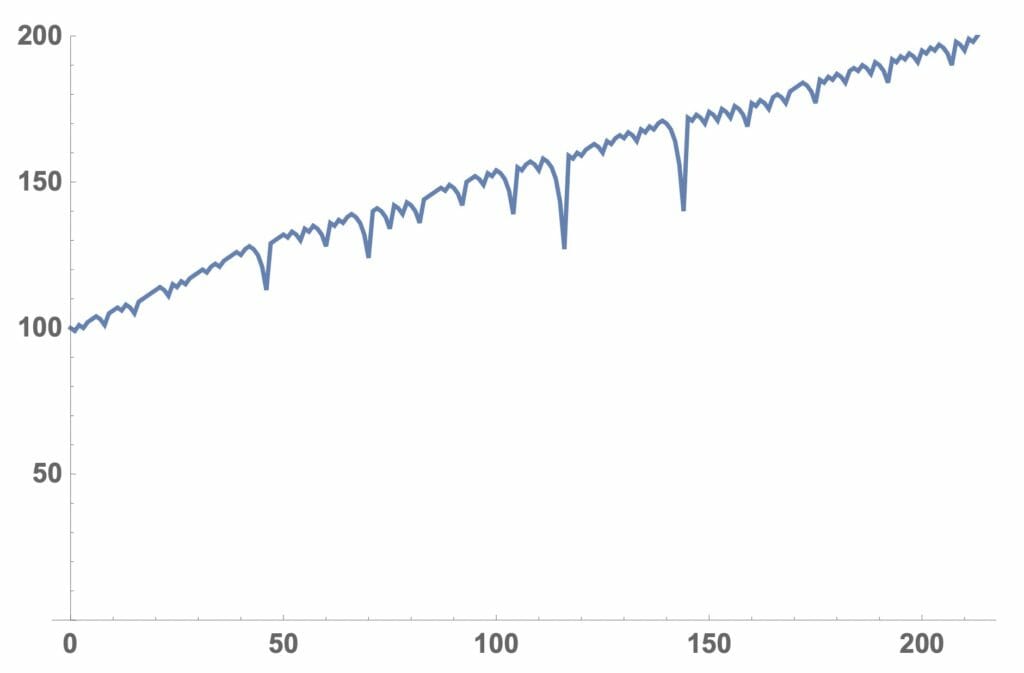
図7ー1:持ち金の変化(2倍になった場合)
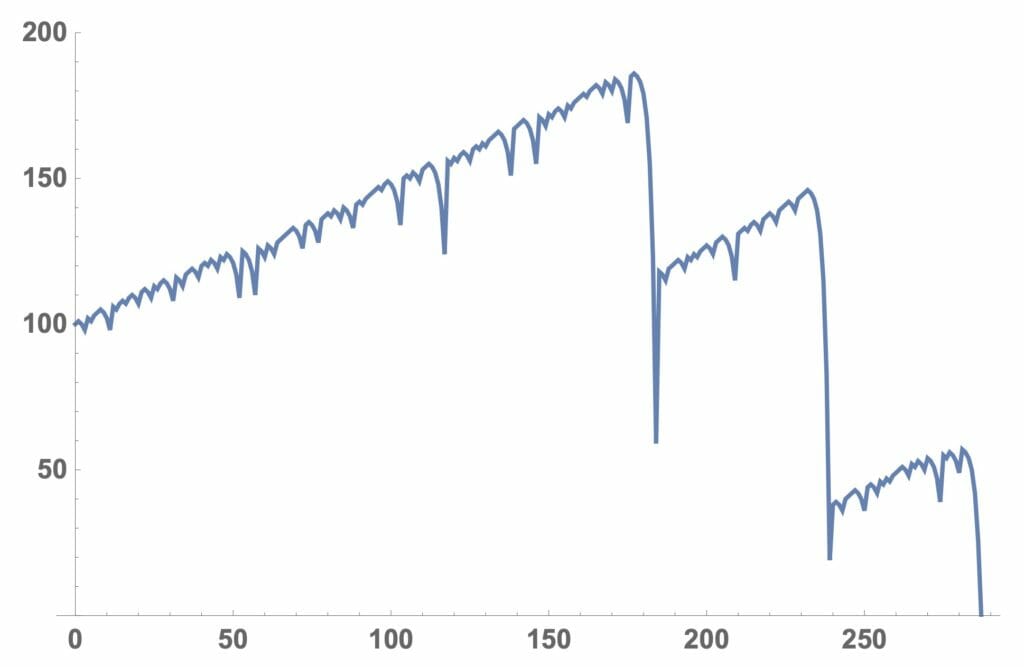
図7ー2:持ち金の変化(無くなった場合)
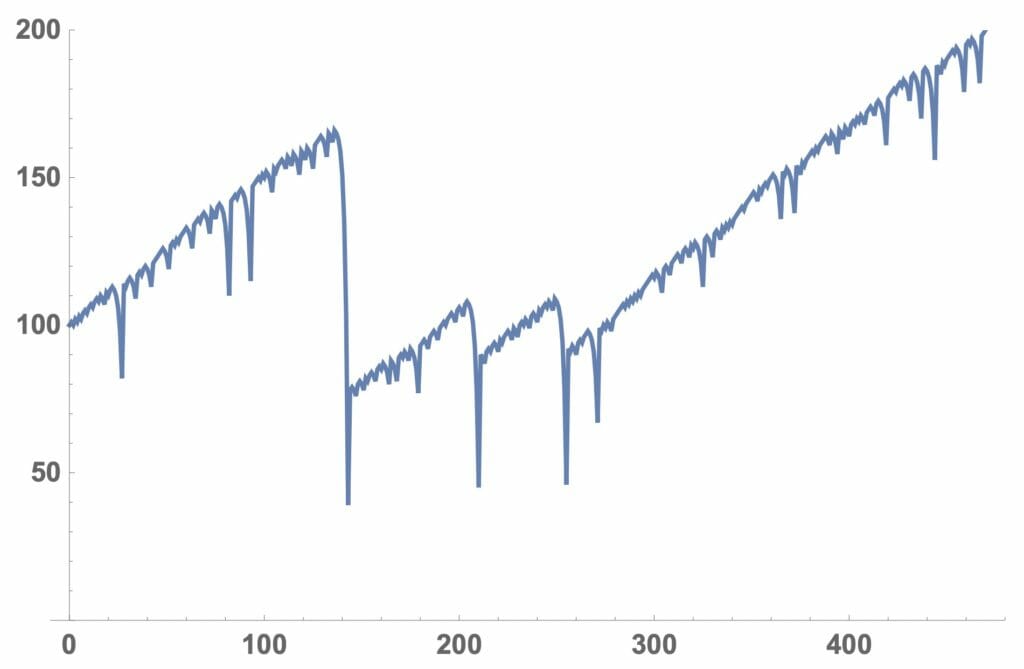
図7ー3:持ち金の変化(途中で持ち直して2倍になった場合)
図7から分かるように持ち金が有限であるために負ける場合があります。従って、
(1)何回ぐらい続けて負けることがあると考えればいいか。
(2)持ち金が倍に成るのに何回ぐらい賭けをしなければならないのか。
(3)勝てる確率はどのくらいか。
という3点について、シミュレーションで検討することにします。
リスト2及びその結果では、roulette2[持ち金、儲けの目標、最小賭け金、シミュレーション回数]で、勝てる確率と2倍になるまで(儲けが持ち金と同じになるまで)行なった賭けの回数の平均を出力する関数を定義し、持ち金を15から255まで5段階に変化させ、1000回のシミュレーションを実行させています。図8に関数の流れ図を示します。
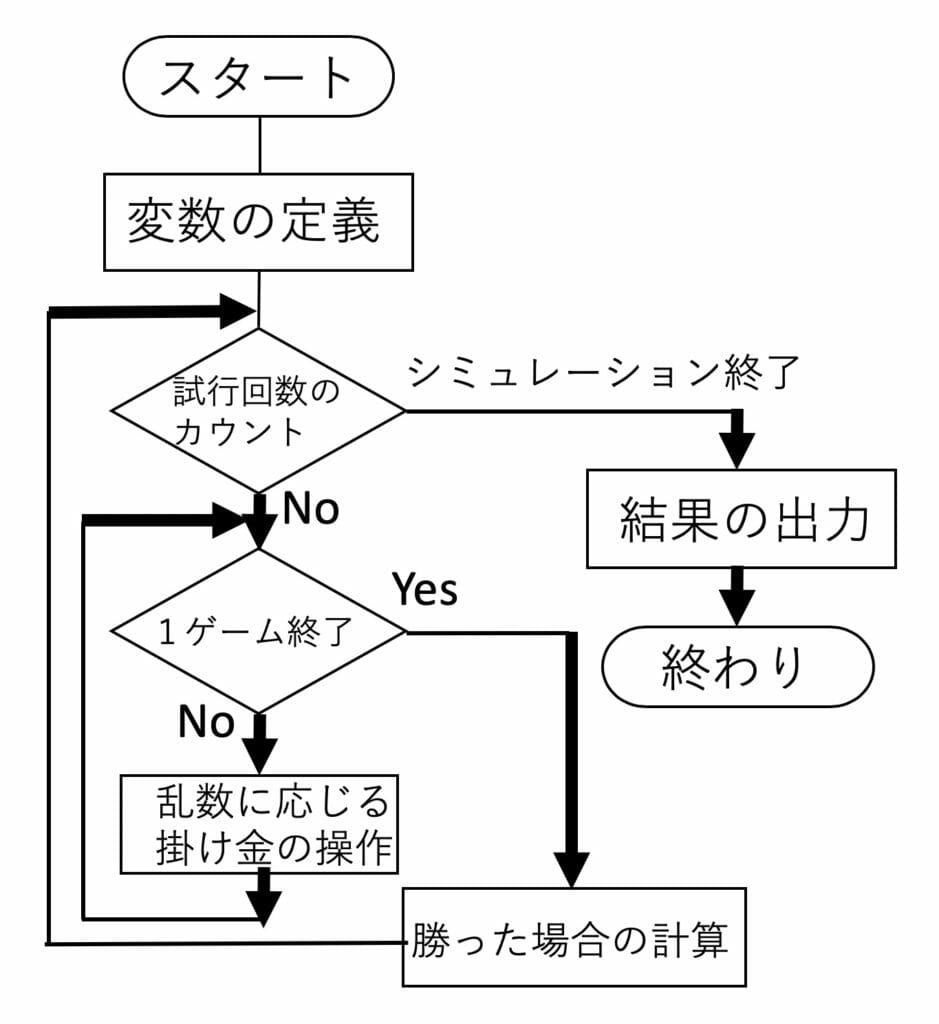
図8:流れ図(roulett2)
<<リスト2及びその結果>>
roulette2[m0_,g0_,p0_,i0_]:= (*関数[持ち金,儲けの目標,最小賭け金,シミュレーション回数]*)
Module[ {m,n,p,s=0,i=0,k=0}, (*変数の定義*)
While[i<i0,i++; (*ループの設定*)
m=m0;n=0;p=p0; (*変数の初期化*)
While[m>0&&m<m0+g0, n++; (*ループの設定*)
If[Random[]<=9/19,m=m+p;p=p0,
m-=p;If[2 p>m,p=m,p=2 p]]; (*乱数に応じる賭け金の操作*)
];
If[m>=m0+g0,s++;k+=n,]; (*勝った場合の計算*)
];
Print[“シミュレーション回数=”,i0]; (*結果の出力*)
Print[“成功率=”,N[s/i0]];
Print[“賭けの回数の平均=”,N[k/s]];
]
SeedRandom[123];
roulette2[15,15,1,1000]
シミュレーション回数=1000
成功率=0.4
賭けの回数の平均=31.4375
SeedRandom[12];
roulette2[31,31,1,1000]
シミュレーション回数=1000
成功率=0.395
賭けの回数の平均=68.1696
SeedRandom[12345];
roulette2[63,63,1,1000]
シミュレーション回数=1000
成功率=0.365
賭けの回数の平均=144.405
SeedRandom[1234];
roulette2[127,127,1,1000]
シミュレーション回数=1000
成功率=0.35
賭けの回数の平均=303.374
SeedRandom[1234567];
roulette2[255,255,1,1000]
シミュレーション回数=1000
成功率=0.297
賭けの回数の平均=626.084
<<リスト3>>
data={{3,0.4,31.4375},{4,.395,68.1696},
{5,0.365,144.405},{6,0.35,303.374},{7,0.297,626.084}};
ListPlot[Table[{data[[i,1]],data[[i,2]]},{i,5}],
PlotJoined->True,PlotRange->{0,0.4}];
ListPlot[Table[{data[[i,1]],data[[i,3]]},{i,5}],
PlotJoined->True,PlotRange->{0,650}]
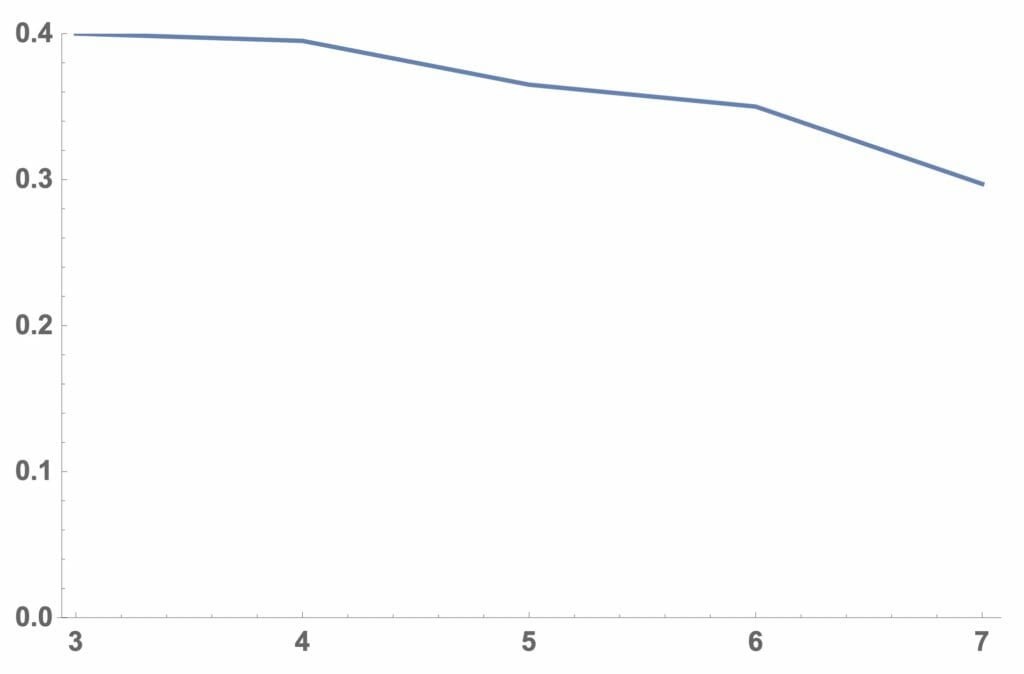
図9:勝つ確率の変化
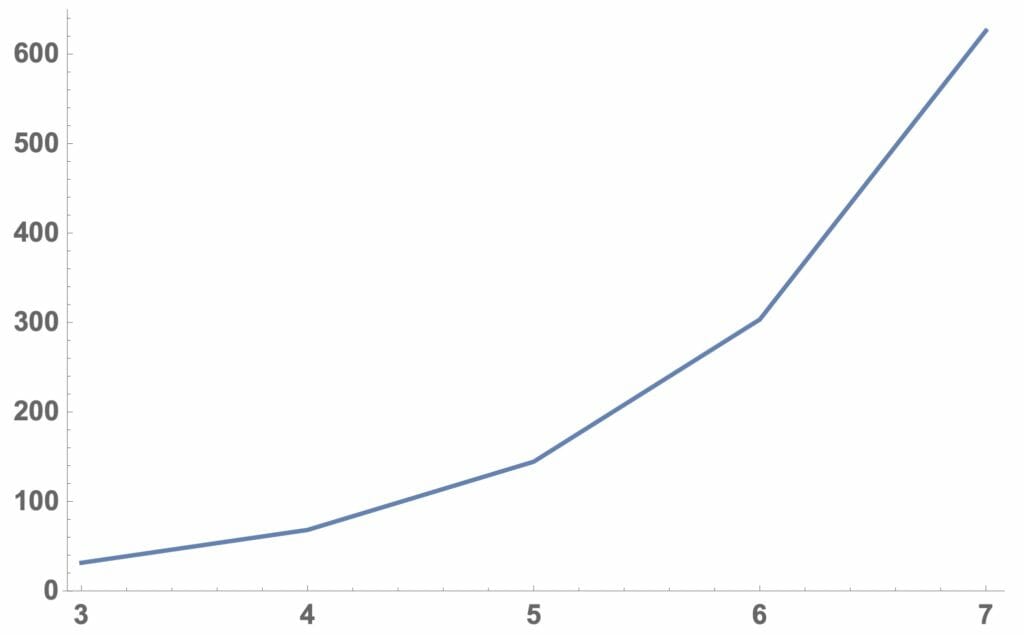
図10:2倍になるまでの賭けの数
4.2 必勝法の検討
リスト3では、リスト2の結果をグラフ化し、図9及び図10を得ました。図9では、連続して負けてもいい回数が増えると勝つ確率が低くなっています。これは、予想に反するものですが、図10から原因は連続して負けてもいい回数が1回増えると持ち金が2倍になるまでに行なわなければならない賭けの回数が2倍以上(約2.2倍)になっているためであろうと解釈できます。
リスト4では、儲けたい金額を一定(15単位)にし、連続して負けてもいい回数を3から7まで変化させ勝つ確率を計算しています。例えば、連続して負けてもいい回数が6以上であれば、勝つ確率は80%以上になっています。もし、80%以上の確率で100ドル儲けたい時には、持ち金に1000ドル用意し5ドルを最小賭け金としてルーレットをやれば良いわけです。大儲けは期待できませんが、勝つ確率が80%以上であれば必勝法と言ってもよいのではないでしょうか。
<<リスト4>>
SeedRandom[123];
roulette2[15,15,1,1000]
シミュレーション回数=1000
成功率=0.4
賭けの回数の平均=31.4375
SeedRandom[123];
roulette2[31,15,1,1000]
シミュレーション回数=1000
成功率=0.579
賭けの回数の平均=32.0915
SeedRandom[123];
roulette2[63,15,1,1000]
シミュレーション回数=1000
成功率=0.74
賭けの回数の平均=31.7081
SeedRandom[123];
roulette2[127,15,1,1000]
シミュレーション回数=1000
成功率=0.856
賭けの回数の平均=30.7301
SeedRandom[123];
roulette2[255,15,1,1000]
シミュレーション回数=1000
成功率=0.92
賭けの回数の平均=31.562
SeedRandom[123];
roulette2[1000,100,5,1000]
シミュレーション回数=1000
成功率=0.861
賭けの回数の平均=48.2869
最後に筆者の体験として、ラスベガスで2日1回ずつ合計2回挑戦する機会がありました。初日は上の通り、サックと気分良く100ドル儲けることが出来ました。次の日は別のホテルで同じように挑戦しましたが、手練れのディラーだったようで、0、00を連発して、負けそうになりました。そこで、金額が大きくなった時は0、00に賭け、持ち直すことが出来ましたが、ディラーが変わり、時間も長くなったので、そこで止め、儲けなしで終了となりました。是非、上のシミュレーションに改良を加えてみて下さい。
4.3 関数の高速化
ところで、シミュレーション回数が多かったため、リストの実行には、最初に行った1990年代のMac SE/30上で約12時間を要しました。Mathematicaで高速化する方法としては、関数をコンパイルし、実行することができます。
リスト5では、関数roulette2をコンパイルし実行させています。この場合、コンパイルにより約70%の時間短縮、つまり、3分の1の時間で実行できています。
<<リスト5>>
roulette2comp= (*関数名*)
Compile[{m0,g0,p0,i0},(*持ち金,儲けの目標,最小賭け金,シミュレーション回数*)
Module[ {m,n,p,s=0,i=0,k=0}, (*変数の定義*)
While[i<i0,i++; (*ループの設定*)
m=m0;n=0;p=p0; (*変数の初期化*)
While[m>0&&m<m0+g0, n++; (*ループの設定*)
If[Random[]<=9/19,m=m+p;p=p0,
m-=p;If[2 p>m,p=m,p=2 p]];(*乱数に応じる賭け金の操作*)
];
If[m>=m0+g0,s++;k+=n,]; (*勝った場合の計算*)
];
Print[“シミュレーション回数=”,i0]; (*結果の出力*)
Print[“成功率=”,N[s/i0]];
Print[“賭けの回数の平均=”,N[k/s]];
]];
SeedRandom[123];
Timing[roulette2comp[15,15,1,1000]]
シミュレーション回数=1000
成功率=0.4
賭けの回数の平均=31.4375
{181.167 Second, Null}
SeedRandom[123];
Timing[roulette2[15,15,1,1000]]
シミュレーション回数=1000
成功率=0.4
賭けの回数の平均=31.4375
{607.583 Second, Null}
※計算結果は当時のMac SE/30のものです。現在ではいずれも10秒以下ですが、例えば精度を2桁上げたいとすれば、回数を1000回から10^7回にあげることになり、簡単に長時間となります。
5 モンテカルロ型シミュレーションの精度
確率的要素を入れて問題を解くときは、常に結果の精度が問題になります。モンテカルロ型シミュレーションによる推定は統計的サンプリングですから、これは常に中心極限定理またはそれを変形した式によって真の値の信頼区間を定めることができます。
それでは、最も簡単な例として最初に例題として上げたπの値を求めるシミュレーションの場合について、その精度を検討します。
この場合、N回の試行回数のうちn回、円の中にはいるとすると、nは実は試行回数N、成功の確率p=π/4の二項分布をする確率変数であることが容易に理解されます。
従って、nの期待値及び標準偏差は、次式で示されます。
期待値 E(n)= Np

このことはN=100とした場合、相対誤差は1/10、つまり1桁合うことを示しています。2桁合わせるためには、N=10000としなければ、なりません。
他の複雑な場合においても同様であり、モンテカルロ法が平均値推定であるため、その精度は試行回数Nの平方根の逆数のオーダーを相対誤差に持つことが、知られています。
なお、モンテカルロ法の精度向上策として層別サンプリングや加重サンプリングなどが知られていますが、これらを複雑なシミュレーションに用いることは困難であり、用いた場合には複雑さをさらに増すものと思いますので、これ以上の説明は省略します。
参考文献
1 岸田孝一・藤井良治「シミュレーションの演習」産報
2 津田孝夫「モンテカルロ法とシミュレーション」培風館
3 関根・高橋・若山ORライブラリー23「シミュレーション」日科技連
4 中村健蔵2019『MathematicaによるOR』楽天Kobo・キンドルDP
ノートブックのダウンロードについて
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。