概要:グラフィックプリミティブ等のMathematicaグラフィックスの基本的な解説は行なったので、Mathematica 2次元Graphicsを具体的に楽しく作りながら、解説していきたい。今回は楕円を使ってキャラクターを作成してみたい。
楕円による作図の利点
Poserという3次元グラフィックのソフトをご存知であろうか?楕円体を基本として動物を精緻に表現できることで有名である。同じ考えで2次元であれば、楕円を使えば思ったよりも簡単にキャラクターを作成できる。Mathematicaで行う利点はプログラムなので何度もやり直しができる点と再利用が簡単な点である。再利用に着いては、途中で説明したい。
図1は昔、娘のぬいぐるみから作ったカッパのKappe君です。プログラム1の通り、楕円をたくさん重ねて作っています。

図1:カッパのKappe君
<<プログラム1>>
Graphics[{RGBColor[.4, 1, .4], Disk[{0, -2}, {.7, 1.2}],(*胴体*)
Disk[{-.7, -1.4}, {.9, .2}], Disk[{.7, -1.4}, {.9, .2}],(*腕*)
RGBColor[0, 0, 0],
Disk[{0, -2.6}, {.8, .6}], Disk[{0, -2.3}, {.8, .6}],(*お尻*)
RGBColor[.4, 1, .4],
Disk[{-1, -2.5}, {1, .5}], Disk[{1, -2.5}, {1, .5}],(*足*)
RGBColor[.4, 1, .4], Disk[{0, 0}, {1.3, 1}],(*頭*)
RGBColor[0, 0, 0],
Disk[{-.3, .45}, .17], Disk[{.3, .45}, .17],(*目*)
Disk[{-.038, -.5}, .04], Disk[{.038, -.5}, .04],(*鼻*)
RGBColor[1, 1, 0], Disk[{0, .95}, {.5, .15}],(*お皿*)
RGBColor[1, 0, 0], Disk[{0, -.7}, {.4, .18}]}](*口*)
イメージの関数化
イメージを再利用しようとすると関数化する必要があります。関数化する際、イメージの中心が{x,y}になる様にします。また、比率rで大きさを定義します。プログラム1でKappe君の座標は、顔の中心を原点{0,0}として定義しています。例えば、口の楕円を書き換えて関数化してみます。
Disk[{0, -.7}, {.4, .18}] ==> Disk[{x, y-r*.7}, r*{.4, .18}]
全てを書き換えたものがプログラム2でkappeという関数として定義しています。図は表示しても同じものですので、ありません。
<<プログラム2>>
kappe[x_,y_,r_:1]:=
{RGBColor[.4,1,.4],Disk[{x,y-r*2},r*{.7,1.2}],(*胴体*)
Disk[{x-r*.7,y-r*1.4},r*{.9,.2}],Disk[{x+r*.7,y-r*1.4},r*{.9,.2}],(*腕*)
RGBColor[0,0,0],Disk[{x,y-r*2.6},r*{.8,.6}], Disk[{x,y-r*2.3},r*{.8,.6}],(*お尻 *)
RGBColor[.4,1,.4],Disk[{x-r,y-r*2.5},r*{1,.5}], Disk[{x+r,y-r*2.5},r*{1,.5}],(*足*)
RGBColor[.4,1,.4],Disk[{x,y},r*{1.3,1}],(*顔*)
RGBColor[0,0,0],
Disk[{x-r*.3,y+r*.45},r*.17], Disk[{x+r*.3,y+r*.45},r*.17],(*目 *)
Disk[{x-r*.038,y-r*.5},r*.04],Disk[{x+r*.038,y-r*.5},r*.04],(*鼻 *)
RGBColor[1,1,0],Disk[{x,y+r*.95},r*{.5,.15}],(*お皿*)
RGBColor[1,0,0],Disk[{x,y-r*.7},r*{.4,.18}]};(*口*)
Show[Graphics[kappe[0,0,1]],
AspectRatio->Automatic,Background->RGBColor[0,0,1]]
関数化イメージの再利用
関数化イメージを再利用したものが、図2です。位置と大きさを変化できるので、曼荼羅状に並べてみました。
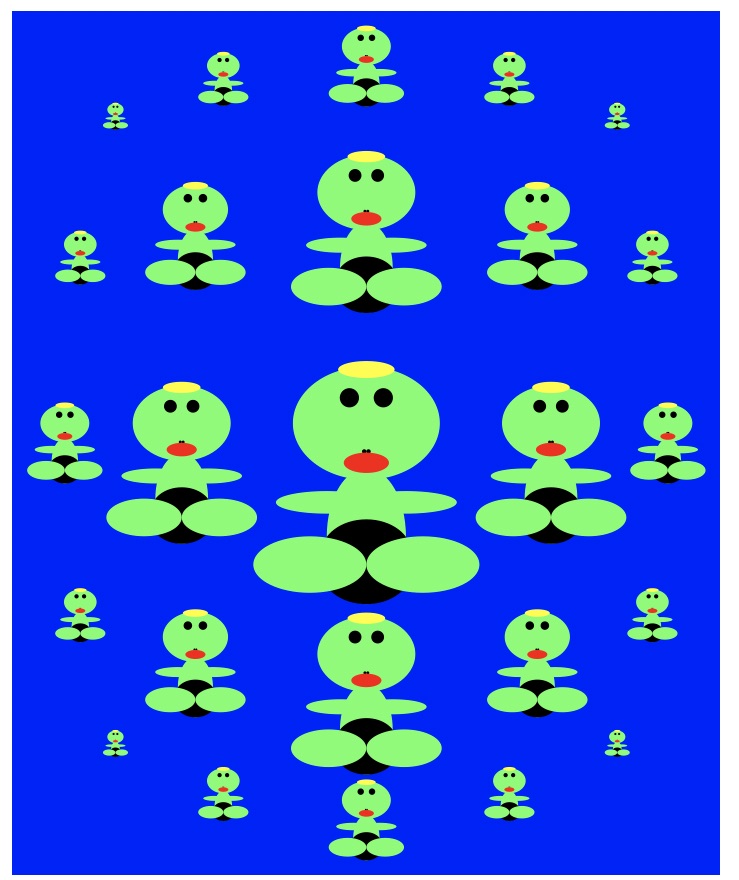
図2:kappe曼陀羅
<<プログラム3>>
a=Table[kappe[8*i/Sqrt[5+i^2+j^2],10*j/Sqrt[5+i^2+j^2],
(3-Abs[i])*(3-Abs[j])/9],{i,-2,2},{j,-2,2}];
Show[Graphics[a],
AspectRatio->Automatic,Background->RGBColor[0,0,1]]
ペンギンのキャラクター
図3左図のピングーを見ながら、作ったら似過ぎたので、ちょっと変えてみたのが、図3中央図です。ここでもう少し改良をして、腕の楕円を傾けてみたものが図3右図です。自然な感じになりました。この時、Rotate[]を使い、楕円を傾けています。
なお、これで作図のレベルは格段に上がります。ただし、試行錯誤の回数が格段に多くなると思われますので、手書きの概略図を先に書くことをお勧めします。
図3:ペンギンのキャラクター
<<プログラム4>>
Penguin[x_,y_,r_:1]:=
{RGBColor[.7,.7,0],Disk[{x-r*.7,y-r*2.7},r*{.5,.25}],
Disk[{x+r*.7,y-r*2.7},r*{.5,.25}],(*足*)
RGBColor[0,0,0],Disk[{x,y-r*1.5},r*{1,1.2}],(*胴体*)
Disk[{x-r*.7,y-r*1.2},r*{.9,.2}],Disk[{x+r*.7,y-r*1.2},r*{.9,.2}],(*腕*)
RGBColor[1,1,0],Disk[{x,y-r*1.65},r*{.8,1}],(* 黄色のお腹*)
RGBColor[1,1,1],Disk[{x,y-r*1.75},r*{.7,.9}],(*お腹*)
RGBColor[0,0,0],Disk[{x,y},r*{.8,.6}],(*頭*)
RGBColor[1,1,1],Disk[{x-r*.5,y+r*.05},r*{.12,.15}], Disk[{x+r*.5,y+r*.05},r*{.12,.15}],(*目*)
RGBColor[0,0,0],Disk[{x-r*.47,y+r*.05},r*.1],
Disk[{x+r*.53,y+r*.05},r*.1],(*目*)
RGBColor[0,0,1],Disk[{x-r*.038,y-r*.5},r*.04],
Disk[{x+r*.038,y-r*.5},r*.04],(*ネクタイ*)
RGBColor[1,1,0],Disk[{x,y-r*.25},r*{.35,.18}]};(*口*)
Show[Graphics[Penguin[0,0,1]],
AspectRatio->Automatic,Background->RGBColor[0,0,1]]
ペンギンのキャラクターの再利用
図4は、ペンギンのキャラクターを再利用し、曼陀羅状に並べたものですが、前回と異なる点は、ペンギンのキャラクターを左右に傾けていることです。これもRotate[]で、-0.25から0.25の乱数を使い左右に傾けてみました。ペンギンがよちよち歩いている雰囲気を狙ったのですが、如何でしょうか!

図4:ペンギンよちよち曼陀羅
<<プログラム5>>
a=Table[Graphics[Rotate[Penguin[8*i/Sqrt[5+i^2+j^2],10*j/Sqrt[5+i^2+j^2],
(3-Abs[i])*(3-Abs[j])/7.5],0.5*(Random[]-.5)]],{i,-2,2},{j,-2,2}];
Show[a,AspectRatio->Automatic,Background->RGBColor[0,.3,1]]
以上、楕円だけでもかなりのことができそうに思って頂ければ嬉しい限りです。自分のキャラクター作りに挑戦してみてください。
参考文献:Mathematicaグラフィックスの入門書
中村健蔵「Mathematicaで絵を描こう」1997東京電機大学出版局
ノートブックのダウンロード
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。