要旨:最も簡単な2次元のグラフィックス・プリミティブである線Lineを使って簡単な図を描くことを解説します。
直線を描くためのグラフィクス・プリミティブLine
点から1つ進んで、直線を描くためのグラフィクス・プリミティブLine[]について解説する。1本の直線は、Line[{{x1,y1},{x2,y2}}]の形式で表わすことが出来る。そして、見た目に変化を与える属性としては、線の太さ、陰影(色)の他に、破線かどうかが考えられる。
最も簡単な例として縦横と斜めの網目2種類を図1、2に示す。
図1:網目(縦横)図2:網目(斜め)
<<プログラム1>>
a=Table[Line[{{i,0},{i,10}}],{i,0,10}];
b=Table[Line[{{0,i},{10,i}}],{i,0,10}];
Show[Graphics[{Thickness[.01],a,b}],AspectRatio->1];(*図1*)
c=Table[Line[{{k,10-i},{i,10-k}}],{i,0,10},{k,0,10,10}];
d=Table[Line[{{k,i},{i,k}}],{i,0,10},{k,0,10,10}];
Show[Graphics[{Thickness[.01],c,d}],AspectRatio->1];(*図2*)
プログラム1の図1では、変数a,bにグラフィクス・プリミティブのリストを代入し、Show[]で作図している。そして、Table[]を用いて{i,0}から{i,10}までiを0から10まで変えて、aのリストを作成している。
斜めの直線の作り方
図2では、斜めの直線のリストを作るときに若干の工夫をしている。まず、Table[]の説明であるが、Table[i,j},{i,1,10},{j,1,10}]により10×10の2次の行列を作ることができる。また、{i,1,10}を{i,1,10,2}にすることにより1つおきの値、つまり、1,3,5,7,9を取ることができる。従って、プログラムにある{k,0,10,10}でkは、0と10の値を取ることになる。これらの工夫により斜めの直線の座標が算定される。下表にcに代入したリストの座標をkが0と10の時にiが0から10まで変わったときの値を掲げた。これから左上がりの斜線のリストが作られる様子が分かって頂けるであろう。
表4:斜めの線の作り方
| k i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| {k,i},{i,k} | 0 | {0,0},{0,0} | {0,1},{1,0} | {0,2},{2,0} | {0,3},{3,0} | {0,4},{4,0} | {0,5},{5,0} | {0,6},{6,0} | {0,7},{7,0} | {0,8},{8,0} | {0,9},{9,0} | {0,10},{10,0} |
| 10 | {10,0},{0,10} | {10,1},{1,10} | {10,2},{2,10} | {10,3},{3,10} | {10,4},{4,10} | {10,5},{5,10} | {10,6},{6,10} | {10,7},{7,10} | {10,8},{8,10} | {10,9},{9,10} | {10,10},{10,10} |
線に陰影(色)を付けた例を図3に示した。更に縦横斜めの線を4つ重ね合せたものが図4である。
図3:陰影の格子 図4:4重陰影の格子
<<プログラム2>>
e=Table[{GrayLevel[Mod[i,11]/10],
Line[{{0,i},{50,i}}],Line[{{i,0},{i,50}}]},{i,0,50}];
Show[Graphics[{Thickness[.01],e}],AspectRatio->1];(*図3*)
a=Table[{Hue[Mod[i,11]/10],Line[{{k,50-i},{i,50-k}}]},{i,0,50},{k,0,50,50}];
b=Table[{Hue[Mod[i,11]/10],Line[{{k,i},{i,k}}]},{i,0,50},{k,0,50,50}];
c=Table[{Hue[Mod[i,11]/10],Line[{{i,0},{i,50}}]},{i,0,50}];
d=Table[{Hue[Mod[i,11]/10],Line[{{0,i},{50,i}}]},{i,0,50}];
Show[Graphics[{Thickness[.005],a,b,c,d}],AspectRatio->1] (*図4*)
カラーと線の太さ
プログラム2の図3では基本的に図1と同じであるが、図1が縦の線を描いた後、横線を描き込んでいるのと異なり、図3では、縦の線を1本書いた後横の線を描くということを繰り返すようにしている。これは線の太さを太くしたため全部の横線を後から上描きすると横線のみが強調されてしまうためである。
線の間隔を変更することも1つの方法であるが、変化が付けにくいので、別の表現方法として原点を通る直線群を考えて見たい。図5に原点を通る直線群を示した。図6には、陰影を付けた図を示す。それぞれに特有の干渉縞のようなものが見られる。
図5:原点を通る直線 図6:原点を通る直線(陰影)
<<プログラム3>>
p=50;
e=Table[Line[{{p-i,0},{i,p}}],{i,0,p}];
f=Table[Line[{{0,p-i},{p,i}}],{i,0,p}];
Show[Graphics[{Thickness[.003],e,f}],AspectRatio->1](*図5*)
p=50;x=3;y=3;
e=Table[{GrayLevel[Mod[i,6]/5],Line[{{i+x,-p+y},{-i+x,p+y}}]},{i,-p,p}];
f=Table[{GrayLevel[Mod[i,6]/5],Line[{{-p+x,i+y},{p+x,-i+y}}]},{i,-p,p}];
Show[Graphics[{Thickness[.003],e,f}],AspectRatio->1](*図6*)
見ていただければ分かるが、プログラム3で斜線を描くのは、ほとんど縦横の線を描くのと同じくらい簡単である。
破線
もう1つの属性である破線にしてみよう。線の定義の前にDashing[{0.05,0.05}]といった形式で置くことで、破線にすることが出来る。与える数値は線を書く部分の長さ0.05、消す部分の長さ0.05を交互に続けることを意味する。したがって、一点鎖線を描きたい場合は、Dashing[{0.01,0.05,0.05,0.05}]とすればよい。(プログラム4もDashing[]の部分だけ変更すればよい)
(破線)(一点鎖線)
図7:破線による作図
<<プログラム4>>
p=50;x=3;y=3;
e=Table[{GrayLevel[Mod[i,6]/5],Dashing[{0.05,0.05}],
Line[{{i+x,-p+y},{-i+x,p+y}}]},{i,-p,p}];
f=Table[{GrayLevel[Mod[i,6]/5],Dashing[{0.05,0.05}],
Line[{{-p+x,i+y},{p+x,-i+y}}]},{i,-p,p}];
Show[Graphics[{Thickness[.003],e,f}],AspectRatio->1]
折れ線
2点をつなげば直線1本であるが、複数の点をつなげていけば折れ線が得られる。折れ線を作るには、Line[{{x1,y1},{x2,y2},・・・,{xn,yn}}]の形式でn点を結んだn-1本の折れ線が作ることが出来る。例えば、図8は天馬のデータをLine[]に与えて表示したものである。
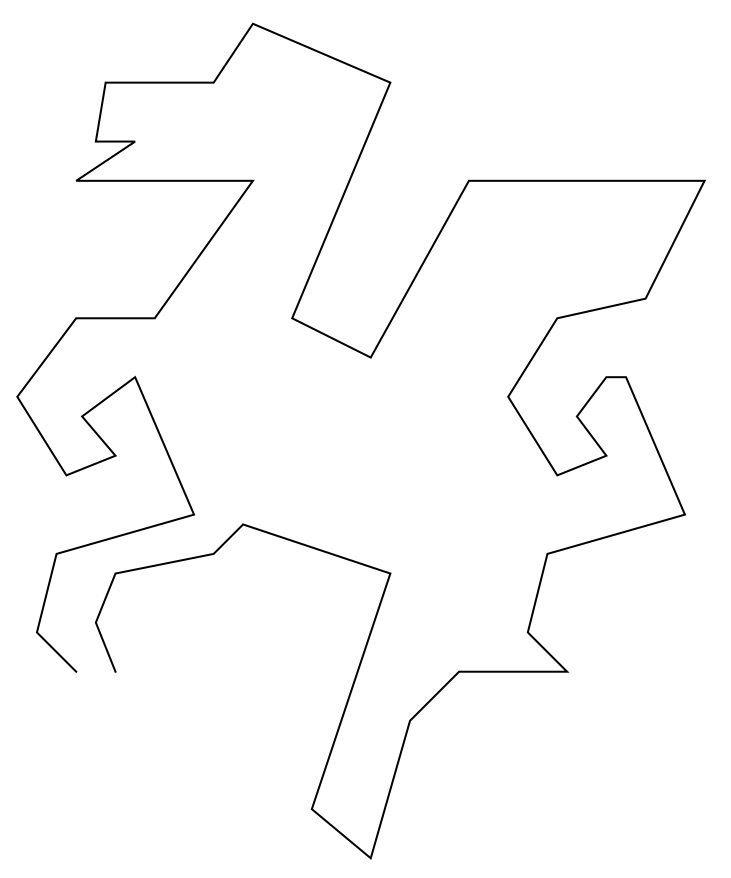
図8:複数の直線による折れ線
<<プログラム5>>
a={{0.3, 0}, {0.1, 0.2}, {0.2, 0.6}, {0.9, 0.8}, {0.6, 1.5}, {0.33, 1.3}, {0.5, 1.1}, {0.25, 1}, {0, 1.4}, {0.3, 1.8}, {0.7, 1.8}, {1.2,2.5}, {0.3, 2.5}, {0.6, 2.7}, {0.4, 2.7}, {0.45, 3.0}, {1, 3}, {1.2, 3.3}, {1.9, 3}, {1.4, 1.8}, {1.8, 1.6}, {2.3,2.5}, {3.5,2.5}, {3.2,1.9}, {2.75,1.8}, {2.5,1.4}, {2.75,1}, {3,1.1}, {2.85,1.3}, {3, 1.5}, {3.1,1.5}, {3.4,0.8}, {2.7,0.6}, {2.6,0.2}, {2.8,0}, {2.25, 0}, {2, -0.25},
{1.8,-0.95}, {1.5, -0.7}, {1.9, 0.5},{1.15, 0.75}, {1, 0.6}, {0.5, 0.5}, {0.4, 0.25}, {0.5, 0}};
Show[Graphics[Line[a]]](*図8*)
線の太さの指定法の違い
ところで、線の太さの指定法として今まで紹介してきたThickness[]の他に、AbsoluteThickness[]を使い指定することができる。Thickness[]が図の大きさの比率で線の太さを指定することと比較して、AbsoluteThickness[]はポイント数(1ポイントは1/72インチ)で線に太さを指定できる。ここで図9を見ていただきたい。
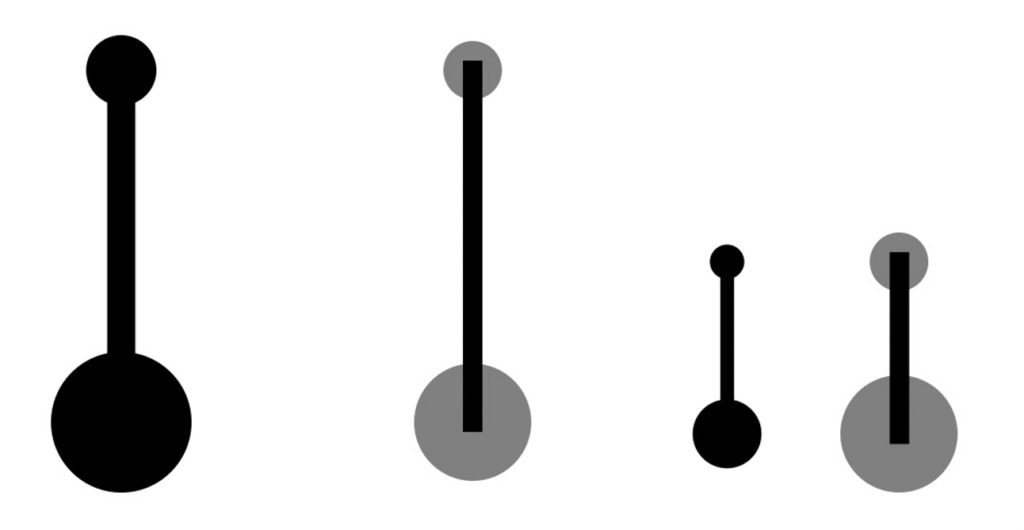
図9:線の太さの指定法の違い
<<プログラム6>>
Show[Graphics[
{Table[{PointSize[0.1*i],Point[{1,2-i}]},{i,1,2}],
Table[{GrayLevel[0.5],AbsolutePointSize[30*i],
Point[{2,2-i}]},{i,1,2}],
{Thickness[.04],Line[{{1,0},{1,1}}]},
{AbsoluteThickness[10],Line[{{2,0},{2,1}}]}}],
AspectRatio->1,PlotRange->{{0.5,2.5},{-0.5,1.5}}];
図9では1.2節で解説した点の大きさとの比較を行うために線だけでなく点も表示しているが、左の大きい図では同じに見える線の太さが図の大きさを半分にすると変わってしまうことになる。ここで注意して頂きたい点は、AbsoluteThickness[]で指定した右側の線についても線の太さは変わらないが、線の長さは変わらざるを得ない訳である。つまり、図形を大きさで絶対的に指定しようとしても、図全体の大きさが変わると変わらざるを得ないのである。従って、前回で述べたように点の大きさだけ考えて、PointSize[]とAbsolutePointSize[]のどちらが使いやすいかは、主観の問題になるかもしれないが、線の太さも含めて考えた場合には、PointSize[]及びThickness[]を使い、相対的に指定したほうが使いやすいことが分かって頂けるのではないだろうか。
なお、この議論は、後で示すの文字列のグラフィクス・プリミティブのところでも再度解説する。
参考文献:Mathematicaグラフィックスの入門書
中村健蔵「Mathematicaで絵を描こう」1997東京電機大学出版局
ノートブックのダウンロード
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。










